
Zadanie maturalne nr 9, matura 2017 (poziom rozszerzony)
Treść zadania:
W trójkącie równoramiennym wysokość opuszczona na podstawę jest równa 36, a promień okręgu wpisanego w ten trójkąt jest równy 10. Oblicz długości boków tego trójkąta i promień okręgu opisanego na tym trójkącie.
 Rozwiązanie zadania
Rozwiązanie zadania
Sporządzamy rysunek poglądowy:
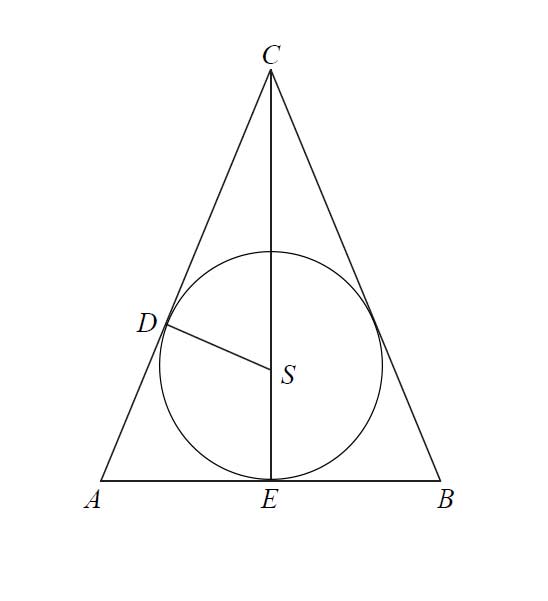
Z warunków zadania wiemy, że |CE|=36, a także, że |DS|=|ES|=10.
Szukamy długości boków trójkąta a=|AB|, b=|BC| i c=|AC|, a także promienia okręgu opisanego na tym trójkącie.
Mamy podaną wysokość trójkąta ABC, obliczymy wszystkie jego boki, zatem korzystając ze wzoru:
łatwo znajdziemy R - promień okręgu opisanego na tym trójkącie.
Trójkąt DSC jest trójkątem prostokątnym, więc z twierdzenia Pitagorasa otrzymujemy:
\( |CS|^2=|DS|^2+|DC|^2 \)
\( |DC|=\sqrt{|CS|^2-|DS|^2}=\sqrt{26^2-10^2}=24 \)
Skąd wiemy, że |CS|=26? Ponieważ |CS|=|CE|-|SE|=36-10=26.
Zauważamy, że trójkąty AEC i SDC mają jeden z kątów wspólny i każdy jest trójkątem prostokątnym. Na podstawie reguły podobieństwa trójkątów kąt-kąt (kk) stwierdzamy, że oba trójkąty są podobne, a stosunki odpowiednich boków są równe. Mamy więc:
\( \frac{|CE|}{|AE|}=\frac{|DC|}{|DS|} \)
\( \frac{36}{|AE|}=\frac{24}{10} \)
\( |AE|=15 \)
Na podstawie twierdzenia o odcinkach stycznych możemy zapisać, że:
\( |AD|=|AE|=15 \)
Zatem długość podstawy wynosi:
\( a=|AB|=30 \)
Mając |AD|=15 i |DS|=24, mamy także boki trójkąta ABC:
\( b=c=|AC|=|BC|=39 \)
Pole trójkąta ABC policzymy ze wzoru na pole trójkąta, gdy dana jest jego podstawa i wysokość.
\( R=\frac{1}{2}\cdot |AB|\cdot |CE|=\frac{1}{2}\cdot 30\cdot 36=540. \)
Promień okręgu opisanego na trójkącie R obliczymy następująco:
\( P=\frac{abc}{4R} \)
\( R=\frac{abc}{4P} \)
\( P=\frac{30\cdot 39\cdot 39}{4\cdot 540}=21\frac{1}{8} \)
 Odpowiedź
Odpowiedź
\( a=30, b=c=39, R=21\frac{1}{8} \)
© medianauka.pl, 2022-12-30, ZAD-4575


Zadania podobne
Zadanie nr 1.
Obliczyć pole i obwód trójkąta prostokątnego, wyznaczonego przez punkty \(A=(1,2), B=(1,3), C=(4,1)\).
Zadanie nr 2.
Oblicz pole powierzchni i obwód trójkąta równobocznego o wysokości \(h=2 cm\).
Zadanie nr 3.
Środki trójkąta równobocznego o boku długości 2 połączono ze sobą tak, że powstał mniejszy trójkąt wewnątrz większego. Obliczyć jego pole.
Zadanie nr 4.
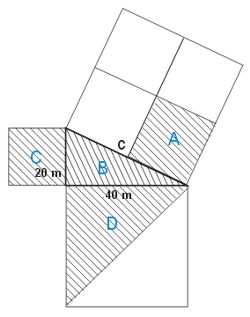
Ceny poszczególnych działek są następujące:
A. 60 000 PLN
B. 50 000 PLN
C. 50 000 PLN
D. 100 000 PLN
Zakup której działki jest najbardziej opłacalny?
Zadanie nr 5.
Dany jest trójkąt o bokach długości 2, 3 i 4. Oblicz pole powierzchni tego trójkąta.
Zadanie nr 6.
Wektory \(\vec{a}=[1,2], \vec{b}=[-3,4]\) wyznaczają trójkąt. Obliczyć jego pole.
Zadanie nr 7.
Dany jest wektor \(\vec{AB}=[2,5]\) zaczepiony w punkcie \(A=(1,1)\). Znaleźć taki punkt \(C\), leżący na prostej \(y=2\), że pole trójkąta \(ABC\) jest równe 10.
Zadanie nr 8.
Dany jest trójkąt równoramienny o ramionach długości 5 i kącie wewnętrznym między tymi ramionami \(\alpha=30°\). Oblicz pole powierzchni tego trójkąta.
Zadanie nr 9.
Na trójkącie o polu równym 6 i o bokach o długości 2, 3 i 4 opisano okrąg. Oblicz długość promienia tego okręgu.
Zadanie nr 10.
Dany jest trójkąt \(A, B, C\) o wierzchołkach \(A=(-1,1), B=(2,1), C=(-2,-1)\). Oblicz jego pole.
Zadanie nr 11.
Z kwadratu o boku a wycięto trójkąt tak, że jeden z jego wierzchołków stanowi środek boku kwadratu, a jeden z boków tego trójkąta stanowi bok kwadratu. Czy pole ścinków jest większe od pola trójkąta?
Zadanie nr 12.
W trójkąt równoramienny o polu \(\sqrt{15}\) wpisano okrąg o promieniu \(r=\frac{\sqrt{15}}{5}\). Na tym samy trójkącie opisano okrąg o promieniu \(R=\frac{8\sqrt{15}}{15}\). Oblicz długości boków tego trójkąta.

Zadanie nr 13 — maturalne.
Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta styczna do okręgu o promieniu 4 w punkcie \(P\) przechodzi przez środek okręgu o promieniu 3 (zobacz rysunek).
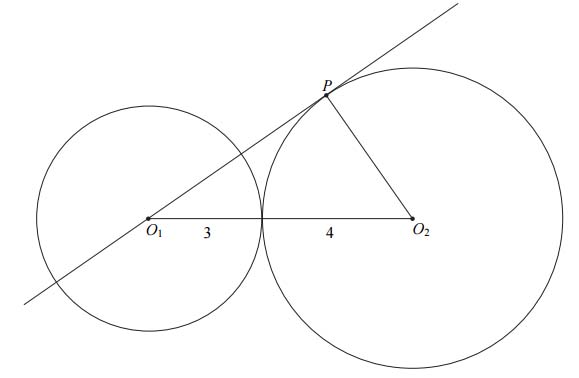
Pole trójkąta, którego wierzchołkami są środki okręgów i punkt styczności \(P\), jest równe:
A. \(14\)
B. \(2\sqrt{33}\)
C. \(4\sqrt{33}\)
D. \(12\)

Zadanie nr 14 — maturalne.
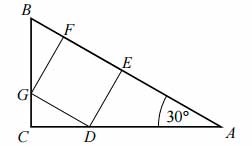
Kąt \(CAB\) trójkąta prostokątnego \(ACB\) ma miarę \(30°\). Pole kwadratu \(DEFG\), wpisanego w ten trójkąt (zobacz rysunek), jest równe 4. Oblicz pole trójkąta \(ACB\).

Zadanie nr 15 — maturalne.
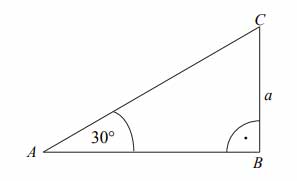
Obwód trójkąta \(ABC\), przedstawionego na rysunku, jest równy:
A. \(3+\frac{\sqrt{3}}{2}\)
B. \(2+\frac{\sqrt{2}}{2}\)
C. \(3+\sqrt{3}\)
D. \((2+\sqrt{2}\)

Zadanie nr 16 — maturalne.
W trójkącie ostrokątnym \(ABC\) bok \(AB\) ma długość \(c\), długość boku \(BC\) jest równa a oraz \(\angle ABC=\beta\). Dwusieczna kąta \(ABC\) przecina bok \(AC\) trójkąta w punkcie \(E\). Wykaż, że długość odcinka \(BE\) jest równa \(\frac{2ac\cdot \cos{\frac{\beta}{2}}}{a+c}\).

Zadanie nr 17 — maturalne.
Przyprostokątna \(AC\) trójkąta prostokątnego ABC ma długość 8 oraz \(tg\alpha=\frac{2}{5}\) (zobacz rysunek).
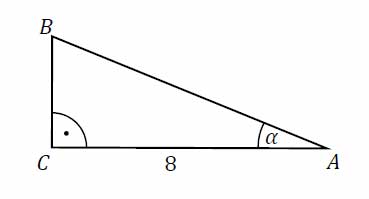
Pole tego trójkąta jest równe
A. \(12\)
B. \(\frac{37}{3}\)
C. \(\frac{62}{5}\)
D. \(\frac{64}{5}\)

Zadanie nr 18 — maturalne.
Punkty \(A=(−20, 12)\) i \(B=(7, 3)\) są wierzchołkami trójkąta równoramiennego ABC, w którym \(|AC|=|BC|\). Wierzchołek \(C\) leży na osi \(Oy\) układu współrzędnych. Oblicz współrzędne wierzchołka \(C\) oraz obwód tego trójkąta.

Zadanie nr 19 — maturalne.
Dany jest trójkąt równoboczny \(ABC\). Na bokach \(AB\) i \(AC\) wybrano punkty — odpowiednio — \(D\) i \(E\) takie, że \(|BD|=|AE=\frac{1}{3}|AB|\). Odcinki \(CD\) i \(BE\) przecinają się w punkcie \(P\) (zobacz rysunek).
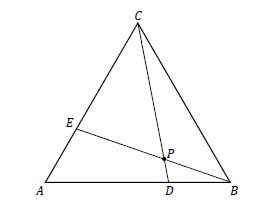
Wykaż, że pole trójkąta \(DBP\) jest 21 razy mniejsze od pola trójkąta \(ABC\).

