Zadanie - pole trójkąta
Treść zadania:
Oblicz pole powierzchni i obwód trójkąta równobocznego o wysokości \(h=2 cm\).
Rozwiązanie zadania
Sporządzamy szkic:
Pole powierzchni trójkąta o podstawie \(a\) i wysokości \(h\) obliczamy ze wzoru:
\(P=\frac{1}{2}ah\)Wysokość jest dana, musimy znaleźć długość boku trójkąta.
Korzystamy z twierdzenia Pitagorasa, które mówi, że w trójkącie prostokątnym kwadrat przeciwprostokątnej jest równy sumie kwadratów przyprostokątnych:
\((\frac{1}{2}a)^2+h^2=a^2\)
\(\frac{1}{4}a^2+h^2=a^2\)
\(a^2-\frac{1}{4}a^2=h^2\)
\(\frac{3}{4}a^2=h^2/:\frac{3}{4}\)
\(a^2=\frac{4}{3}h^2\)
\(a=\sqrt{\frac{4}{3}h^2}\)
\(a=\frac{2h}{\sqrt{3}}\)
\(a=\frac{2\sqrt{3}}{3}\cdot h\)
\(a=\frac{2\sqrt{3}}{3}\cdot 2\ cm\)
\(a=\frac{4\sqrt{3}}{3}\ cm\)
Obliczamy pole trójkąta:
\(P=\frac{1}{2}ah= \frac{1}{\cancel{2}}\cdot \frac{4\sqrt{3}}{3}\ cm \cdot \cancel{2} \ cm= \frac{4\sqrt{3}}{3}\ cm^2\)
Obwód trójkąta obliczymy, dodając do siebie długości trzech boków.
\(L=3a=\cancel{3}\cdot \frac{4\sqrt{3}}{\cancel{3}} \ cm=4\sqrt{3} \ cm\)
Odpowiedź
\(P=\frac{4\sqrt{3}}{3}, \ L=4\sqrt{3}\)© medianauka.pl, 2011-02-11, ZAD-1145


Zadania podobne
Zadanie nr 1.
Przez punkty \(A, B\) na okręgu o promieniu \(r=2,5\) poprowadzono średnicę. Punkt \(D\) leży na okręgu tak, że \(|BD|=4\). Oblicz odległość \(|AD|\).
Zadanie nr 2.
Oblicz wysokość w trójkącie równoramiennym o ramionach długości 10 i o podstawie długości 12.
Zadanie nr 3.
W trójkącie równoramiennym o ramionach długości 5 wysokość ma długość 4. Oblicz długość podstawy.
Zadanie nr 4.
W trójkącie prostokątnym miary dwóch kątów wewnętrznych są równe, a długość przeciwprostokątnej jest równa 6. Oblicz miarę kątów w tym trójkącie oraz długość boków.
Zadanie nr 5.
W trójkącie prostokątnym długości przyprostokątnych wynoszą odpowiednio 5 i 8. Oblicz długość przeciwprostokątnej.
Zadanie nr 6.
Znaleźć dowolny trójkąt prostokątny, dla którego kwadrat krótszej przyprostokątnej jest równy 1/4 kwadratu przeciwprostokątnej.
Zadanie nr 7.
Dane są kwadraty o polach \(\frac{1}{4}\) oraz \(\frac{1}{9}\). Jakie pole ma trzeci kwadrat, jeżeli wiadomo, że z ich boków można skonstruować trójkąt prostokątny?
Zadanie nr 8.
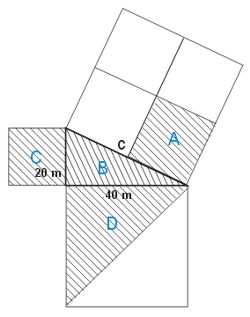
Ceny poszczególnych działek są następujące:
A. 60 000 PLN
B. 50 000 PLN
C. 50 000 PLN
D. 100 000 PLN
Zakup której działki jest najbardziej opłacalny?

Zadanie nr 10 — maturalne.
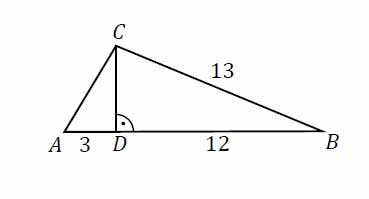
W trójkącie \(ABC\) bok \(BC\) ma długość 13, a wysokość \(CD\) tego trójkąta dzieli bok \(AB\) na odcinki o długościach \(|AD|=3\) i \(|BD|=12\) (zobacz rysunek obok). Długość boku \(AC\) jest równa
A. \(\sqrt{34}\)
B. \(\frac{13}{4}\)
C. \(2\sqrt{14}\)
D. \(3\sqrt{45}\)

