Okrąg wpisany w trójkąt
Okrąg wpisany w trójkąt (wielokąt wypukły) jest to okrąg, którego środek należy do wnętrza trójkąta (wielokąta wypukłego) i który jest styczny do prostych zawierających boki tego trójkąta (wielokąta).
Poniższy rysunek przedstawia okręgi wpisane w trójkąt i czworokąt oraz pięciokąt foremny.
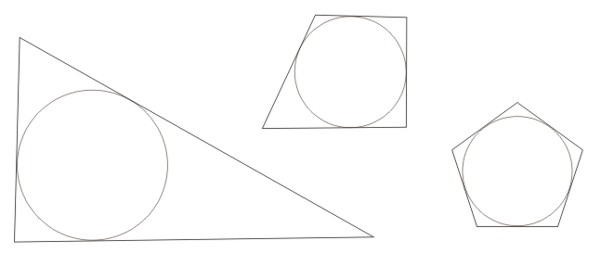
Jeśli okrąg wpisany w wielokąt jest brzegiem koła, to takie koło nazywamy kołem wpisanym w wielokąt, wielokąt zaś — wielokątem opisanym na kole.
Twierdzenie
Dwusieczne kątów trójkąta przecinają się w jednym punkcie, który jest środkiem okręgu wpisanego w ten trójkąt.
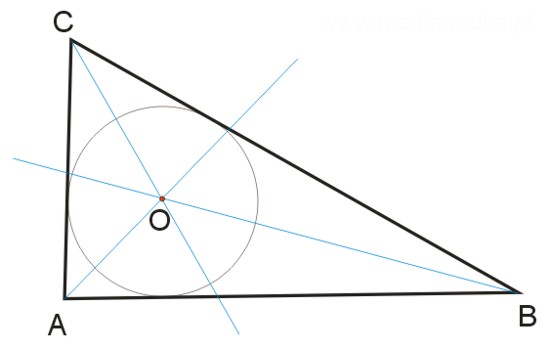
Konstrukcja okręgu wpisanego w trójkąt
Konstrukcja okręgu wpisanego w trójkącie sprowadza się do konstrukcji trzech dwusiecznych kątów trójkąta. W ten sposób wyznaczamy środek okręgu. Promień okręgu leży na prostej prostopadłej do boku trójkąta, przechodzącej przez środek okręgu (rzutujemy prostopadle środek okręgu na bok trójkąta). Konstrukcję okręgu wpisanego w trójkąt można prześledzić na poniższym filmie.
Okrąg wpisany w trójkąt — wzory
W kilku przypadkach możemy zastosować wzory do obliczenia promienia okręgu wpisanego w trójkąt.
Okrąg wpisany w trójkąt równoboczny
Przedstawiamy wzór na promień okręgu wpisanego w trójkąt równoboczny o boku długości \(a\).
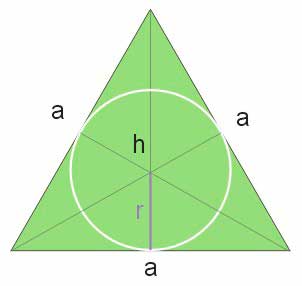
W przypadku trójkąta równobocznego dwusieczne kątów wewnętrznych zawierają wysokości trójkąta. Wysokości, jak już wyżej napisano, przecinają się w środku ciężkości trójkąta, który dzieli wysokość w stosunku 2:1.
Okrąg wpisany w trójkąt prostokątny
Przedstawiamy wzór na promień okręgu wpisanego w trójkąt prostokątny o przeciwprostokątnej długości c.
Pytania
Czy w trójkąt równoramienny rozwartokątny można wpisać okrąg?
W każdy trójkąt można wpisać okrąg.
Zadania z rozwiązaniami

Zadanie nr 1.
Wyznaczyć środek okręgu wpisanego w trójkąt wyznaczony przez punkty \(A=(0,0), B=(4,0), C=(0,3)\).

Zadanie nr 2 — maturalne.
W trójkącie równoramiennym wysokość opuszczona na podstawę jest równa 36, a promień okręgu wpisanego w ten trójkąt jest równy 10. Oblicz długości boków tego trójkąta i promień okręgu opisanego na tym trójkącie.

Zadanie nr 3 — maturalne.
Dany jest trójkąt prostokątny \(ABC\). Promień okręgu wpisanego w ten trójkąt jest pięć razy krótszy od przeciwprostokątnej tego trójkąta. Oblicz sinus tego z kątów ostrych trójkąta \(ABC\), który ma większą miarę.
Powiązane materiały
 Okrąg wpisany w trójkąt
Okrąg wpisany w trójkąt© medianauka.pl, 2010-11-15, A-1018
Data aktualizacji artykułu: 2023-06-14

 Okrąg opisany na trójkącie
Okrąg opisany na trójkącie Okrąg dopisany do trójkąta
Okrąg dopisany do trójkąta Okrąg opisany, dopisany i wpisany w trójkąt
Okrąg opisany, dopisany i wpisany w trójkąt Okrąg i koło
Okrąg i koło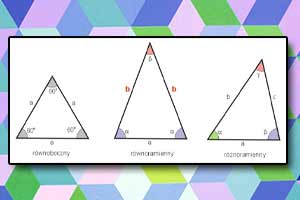 Trójkąty
Trójkąty