Okrąg dopisany do trójkąta

Okrąg dopisany do trójkąta jest to okrąg, którego środek leży na zewnątrz trójkąta i który jest styczny do prostych zawierających boki tego trójkąta.

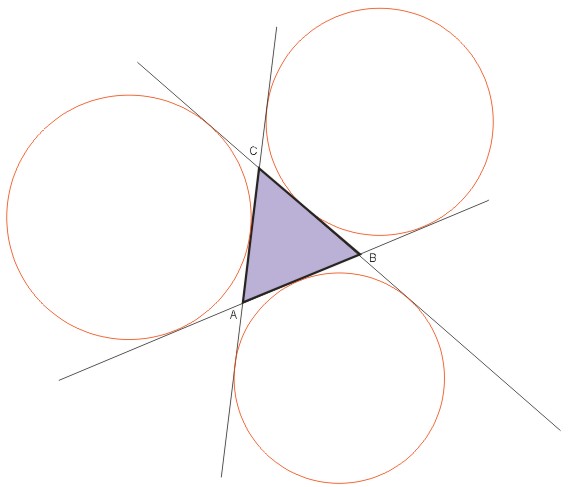
okrąg dopisany do trójkąta

Każdy trójkąt ma trzy okręgi dopisane. Każdy okrąg dopisany ma jeden punkt wspólny z trójkątem.

Twierdzenie

Środek okręgu dopisanego do trójkąta jest punktem przecięcia się dwusiecznych kątów zewnętrznych przy wierzchołkach i dwusiecznej kąta wewnętrznego przy trzecim wierzchołku.

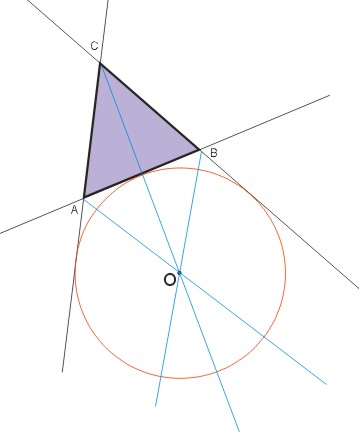
okrąg dopisany do trójkąta - konstrukcja

Zatem, aby narysować okrąg dopisany do trójkąta, należy wykreślić przynajmniej dwie dwusieczne, jedną kąta wewnętrznego z wierzchołka najbardziej oddalonego oraz kąta zewnętrznego z wierzchołka boku stycznego z okręgiem. Ilustruje to powyższy rysunek.

Powiązane materiały

Okrąg wpisany w trójkąt

Okrąg opisany na trójkącie

Okrąg opisany, dopisany i wpisany w trójkąt

Okrąg i koło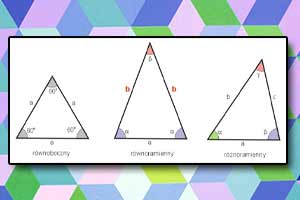

Trójkąty