Twierdzenia o trójkącie

Najlepiej znane twierdzenie o trójkącie to twierdzenie Pitagorasa, któremu poświęcamy osobny artykuł. Wiele innych twierdzeń omawiamy w artykułach o trójkątach. Tutaj prezentujemy rzadziej spotykane w podręcznikach twierdzenia o trójkątach.

Twierdzenie 1

Odcinek, który łączy środki dwóch boków trójkąta, jest równoległy do trzeciego boku, a jego długość jest równa połowie tego boku.

Dowód tego twierdzenia jest prosty i oparty jest na własności działań na wektorach.

Dowód

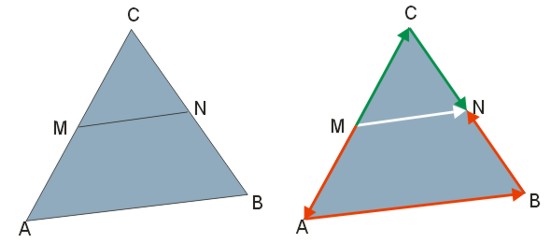
dowód twierdzenia

Korzystamy z sumy wektorów i dodajemy stronami równania:

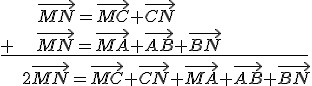
$\vec{MN}=\vec{MC}+\vec{CN}\\ \underline{+ \vec{MN}=\vec{MA}+\vec{AB}+\vec{BN}}2\vec{MN}=\vec{MC}+\vec{CN}+\vec{MA}+\vec{AB}+\vec{BN}$

Uporządkujemy wyrazy po prawej stronie równania:

$2\vec{MN}=(\vec{MC}+\vec{MA})+(\vec{CN}+\vec{BN})+\vec{AB}$

Wektory ujęte parami w nawiasach są wektorami przeciwnymi, więc:

$2\vec{MN}=\vec{0}+\vec{0}+\vec{AB}$

$ 2\vec{MN}=\vec{AB}$

$ \vec{MN}=\frac{1}{2}\vec{AB}$

Zgodnie z definicją mnożenia wektora przez skalar (liczbę), wektory te są równoległe, mają ten sam zwrot, a długość jednego jest o połowę mniejsza niż drugiego, co należało dowieść.

Punkt Gergonne'a

W dowolnym trójkącie proste łączące wierzchołki trójkąta z punktami styczności okręgu wpisanego w ten trójkąt z bokami przeciwległymi przecinają się w jednym punkcie, który nazywamy punktem Gergonne'a.

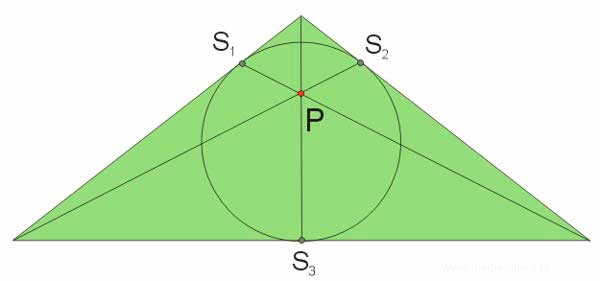
punkt Gergonne'a

Współliniowość punktów w trójkącie

W dowolnym trójkącie środek ciężkości ($S_1$), środek okręgu opisanego ($S_2$), środek okręgu przechodzącego przez środki boków ($S_3$) i ortocentrum ($S_4$) są współliniowe.

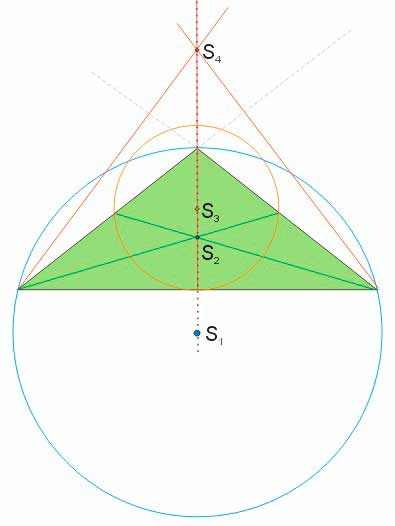
ilustracja twierdzenia

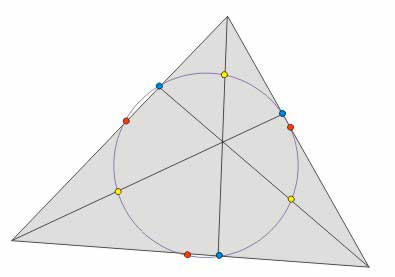
Okrąg Eulera

W dowolnym trójkącie środki boków (czerwone), spodki wysokości (niebieskie), środki odcinków, łączących ortocentrum z wierzchołkami (żółte) leżą na jednym okręgu, który nazywamy okręgiem dziewięciu punktów lub okręgiem Eulera.

okrąg Eulera

Zadania z rozwiązaniami

Zadanie nr 1.

Dany jest trójkąt $ABC$ o bokach długości: $|AB|=6, |BC|=4, |AC|=5$. Punkt $M$ jest środkiem boku $AC$, punkt $N$ — środkiem boku $BC$. Obliczyć obwód trapezu $ABNM$.

Pokaż rozwiązanie zadania.