Figury przystające

Co to są figury przystające? Jakie są cechy przystawania? Zacznijmy od definicji przystawania.

Dwie figury \(f\) i \(g\) nazywamy figurami przystającymi, jeżeli istnieje izometria, która przekształca jedną figurę w drugą. Używamy wówczas następującego zapisu: \(f≡g\).

Istnieją pewne własności, które pozwalają określić, czy dane figury są przystające, czy nie. Reguły te nazywamy cechami przystawania. Aby dowieść, że dwie figury są przystające, wystarczy znaleźć izometrię, która przekształca jedną figurę w drugą.

Przykłady

Poniżej zilustrowano dwie figury przystające. Wystarczy dokonać przesunięcia jednej z nich i obrotu, aby przekształcić jedną figurę w drugą.

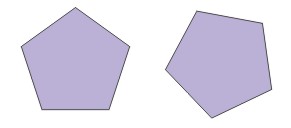
figury przystające

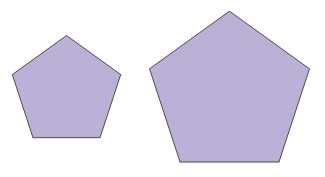
Poniżej znajduje się przykład figur, które nie są przystające. Nie można znaleźć takiego przekształcenia, które zachowuje odległości (czyli izometrii), aby przekształcić jedną figurę w drugą.

figury nieprzystające

Trójkąty przystające

Oto cechy przystawania trójkątów.

Cecha bbb (bok-bok-bok)

Dwa trójkąty są przystające, jeżeli trzy boki jednego trójkąta są odpowiednio równe trzem bokom drugiego trójkąta.

Cecha bkb (bok-kąt-bok)

Dwa trójkąty są przystające, jeżeli dwa boki i kąt między nimi jednego trójkąta są odpowiednio przystające do dwóch boków i kąta zawartego między tymi bokami w drugim trójkącie.

Cecha kbk (kąt-bok-kąt)

Dwa trójkąty są przystające, jeżeli bok i dwa kąty, leżące przy nim w jednym trójkącie są odpowiednio przystające do boku i kątów leżących przy tym boku w drugim trójkącie.

Przykład

Wykazać, że dwa trójkąty, wyznaczone przez przekątną w prostokącie, są przystające.

Sporządzamy rysunek:

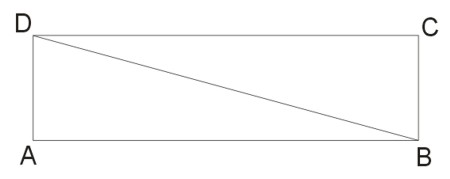
Rysunek

Skorzystajmy z cechy bkb. Kąty \(\angle DAB\) i \(\angle DCB\) są przystające (spróbuj znaleźć izometrię, która przekształca jeden kąt w drugi), a odpowiednie boki zawierające się w ramionach tych kątów z definicji prostokąta są równe: \(|AD|=|BC|\) i \(|AB|=|CD|\). Ponieważ spełniona jest cecha bkb, to trójkąty \(ABD\) i \(BCD\) są przystające.

Cecha przystawania odcinków

Odcinki są przystające, jeśli są równe (mają równe długości).

Przykład

Dwa dowolne boki kwadratu są przystające, ponieważ długości wszystkich boków kwadratu są takie same. Natomiast w prostokącie tylko wybrane boki są przystające.

Cecha przystawania okręgów

Okręgi są przystające, jeśli mają równe promienie.

Ćwiczenia

Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.

ĆWICZENIA

Przystawanie figur

Zadania z rozwiązaniami

Zadanie nr 1.

Dany jest trójkąt równoboczny o boku a. Środki boków tego trójkąta dzielą dany trójkąt na mniejsze części. Wykaż, że wszystkie mniejsze trójkąty są przystające i są trójkątami równobocznymi.

Pokaż rozwiązanie zadania.

Zadanie nr 2 — maturalne.

Dany jest prostokąt \(ABCD\). Okrąg wpisany w trójkąt \(BCD\) jest styczny do przekątnej \(BD\) w punkcie \(N\). Okrąg wpisany w trójkąt \(ABD\) jest styczny do boku \(AD\) w punkcie \(M\), a środek \(S\) tego okręgu leży na odcinku \(MN\), jak na rysunku.

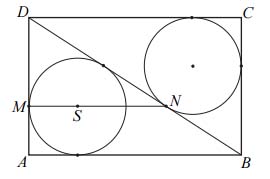
Ilustracja do zadania 9 z oznaczeniami

Wykaż, że \(|MN|=|AD|\).

Pokaż rozwiązanie zadania.

Inne zagadnienia z tej lekcji

Podobieństwo i figury podobne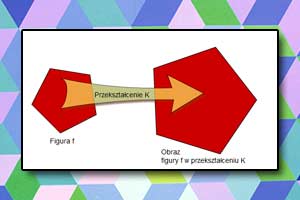

Przekształcenie geometryczne

Trójkąt

Twierdzenia o trójkącie