Trójkąt równoboczny

Co to jest trójkąt równoboczny? Oto definicja tego trójkąta.

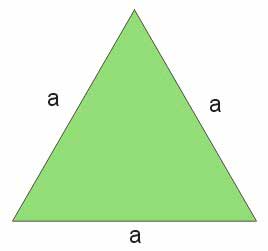
Trójkąt równoboczny jest to trójkąt, w którym wszystkie boki są równe.

Jak wygląda trójkąt równoboczny? Ilustruje go poniższy rysunek.

trójkąt równoboczny

Własności trójkąta równobocznego

Przedstawiamy kilka ważnych twierdzeń i wzory przydatne przy rozwiązywaniu zadań, w których pojawiają się trójkąty równoboczne.

Twierdzenie 1 - Kąty w trójkącie równobocznym.

Miara wszystkich kątów wewnętrznych w trójkącie równobocznym jest równa 60^o.

Twierdzenie 2

W trójkącie równobocznym dwusieczne kątów wewnętrznych zawierają wysokości tego trójkąta.

Twierdzenie 3

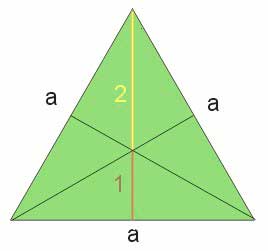
Środkowa w trójkącie równobocznym jest jednocześnie wysokością. Środkowe i wysokości trzech boków przecinają się w jednym punkcie, który nazywamy środkiem ciężkości trójkąta. Środek ciężkości dzieli każdą ze środkowych w stosunku 2:1.

środkowe w trójkącie równobocznym

Wysokość w trójkącie równobocznym

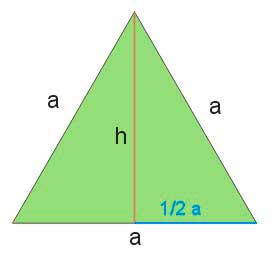
Wysokość \(h\) trójkąta równobocznego dzieli go na dwa trójkąty prostokątne, których jedna przyprostokątna ma długość równą długości wysokości, druga przyprostokątna ma długość równą połowie długości boku trójkąta równobocznego, natomiast przeciwprostokątna ma długość równą długości boku trójkąta równobocznego \(a\). Długość wysokości obliczymy, korzystając z twierdzenia Pitagorasa:

\(a^2=h^2+(\frac{1}{2}a)^2\)

\(a^2-(\frac{1}{2})^2=h^2\)

\(h^2=a^2-\frac{1}{4}a^2\)

\(h^2=\frac{3}{4}a^2\)

\(h=\sqrt{\frac{3}{4}a^2}\)

\( h=\frac{1}{2}a\sqrt{3}\)

wysokość trójkąta równobocznego

Zatem wzór na wysokość w trójkącie równobocznym jest następujący:

\(d=\frac{a\sqrt{3}}{2}\)

Powyższy wzór pozwala obliczyć wysokość \(h\) w trójkącie równobocznym.

Pole trójkąta równobocznego

Pole powierzchni dowolnego trójkąta wyraża się wzorem: \(P=\frac{1}{2}ah\), gdzie \(a\) jest długością boku trójkąta, a \(h\) jego wysokością. Ponieważ wyżej wyznaczyliśmy wysokość trójkąta, możemy wyrazić pole powierzchni trójkąta równobocznego tylko w zależności od długości jego boku.

\(P=\frac{1}{2}ah=\frac{1}{2}a\cdot \frac{1}{2}a\sqrt{3}=\frac{a^2\sqrt{3}}{4}\)

Zatem pole powierzchni trójkąta równobocznego wyraża się wzorem:

\(P=\frac{a^2\sqrt{3}}{4}\)

Przykład

Jakie pole ma trójkąt równoboczny o obwodzie 12?

Jeżeli obwód \(L=12\), to bok trójkąta równobocznego ma długość \(a=\frac{12}{3}=4\).

Zatem pole \(P=\frac{a^2\sqrt{3}}{4}=4\sqrt{3}\).

Obwód trójkąta równobocznego

Jeżeli długość boku trójkąta równobocznego wynosi \(a\), to obwód \(L\) tego trójkąta jest równy:

\(L=3a\)

Promień okręgu wpisanego w trójkąt równoboczny

Długość promienia okręgu wpisanego w trójkąt równoboczny

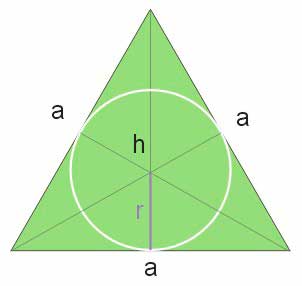
Dwusieczne kątów trójkąta przecinają się w jednym punkcie, który jest środkiem okręgu wpisanego w ten trójkąt. W przypadku trójkąta równobocznego dwusieczne kątów wewnętrznych zawierają wysokości trójkąta. Wysokości, jak już wyżej napisano, przecinają się w środku ciężkości trójkąta, który dzieli wysokość w stosunku 2:1. Promień okręgu wpisanego w trójkąt równoboczny jest równy jednej trzeciej wysokości trójkąta równobocznego, którą wcześniej wyznaczyliśmy.

\(r=\frac{1}{3}h=\frac{1}{3}\cdot \frac{1}{2}a\sqrt{3}=\frac{a\sqrt{3}}{6}\)

Zatem długość promienia okręgu wpisanego w trójkąt równoboczny wyraża się wzorem:

\(r=\frac{a\sqrt{3}}{6}\)

Promień okręgu opisanego na trójkącie równobocznym

Długość promienia okręgu opisanego na trójkącie równobocznym

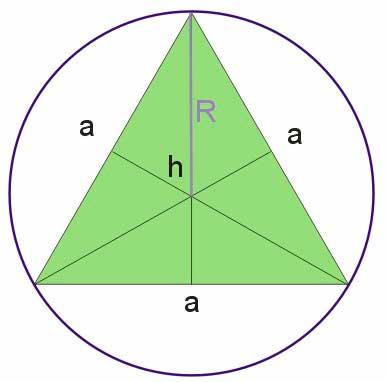
Symetralne boków trójkąta przecinają się w jednym punkcie, który jest środkiem okręgu opisanego w ten trójkąt. W przypadku trójkąta równobocznego symetralne boków zawierają wysokości trójkąta. Środek okręgu wpisanego w trójkąt jest jednocześnie środkiem okręgu opisanego na tym trójkącie. Wysokości, jak już wyżej napisano, przecinają się w środku ciężkości trójkąta, który dzieli wysokość w stosunku 2:1. Promień okręgu wpisanego w trójkąt równoboczny jest równy dwóm trzecim wysokości trójkąta równobocznego, którą wcześniej wyznaczyliśmy.

\(R=\frac{2}{3}h=\frac{\cancel{2}}{3}\cdot \frac{1}{\cancel{2}}a\sqrt{3}=\frac{a\sqrt{3}}{3}\)

Zatem długość promienia okręgu opisanego na trójkącie równobocznym wyraża się wzorem:

\(R=\frac{a\sqrt{3}}{3}\)

Pytania

Dlaczego nie istnieje trójkąt prostokątny równoboczny?

W trójkącie prostokątnym jeden z kątów zgodnie z definicją trójkąta prostokątnego musi mieć 90°, a w trójkącie równobocznym prostokątnym wszystkie kąty wewnętrzne musiałyby mieć miarę 90° (zgodnie z własnościami trójkąta równobocznego). Suma kątów w każdym trójkącie jest równa 180°, a 3·90° = 270°.

Ile osi symetrii ma trójkąt równoboczny?

Trójkąt równoboczny ma trzy osie symetrii. Wszystkie zawierają wysokość tego trójkąta.

Co to jest trójkąt foremny?

Jest to trójkąt równoboczny. Nazwa wywodzi się stąd, że trójkąt równoboczny jest jedynym trójkątem, który jest wielokątem foremnym.

Jak narysować trójkąt równoboczny?

Wystarczy narysować podstawę o zadanej długości i cyrklem o rozwartości na długość tej podstawy narysować z końców podstawy dwa przecinające się łuki, które wyznaczą trzeci wierzchołek szukanego trójkąta.

Ćwiczenia

Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.

ĆWICZENIA

Trójkąty równoboczne

Zadania z rozwiązaniami

Zadanie nr 1.

Na trójkącie równobocznym o boku \(a=1\) opisano okrąg. Oblicz obwód tego okręgu i pole koła wyznaczonego przez ten okrąg.

Pokaż rozwiązanie zadania.

Zadanie nr 2.

W trójkąt równoboczny o boku długości \(a=1\) wpisano koło. Oblicz jego pole i obwód.

Pokaż rozwiązanie zadania.

Zadanie nr 3.

Dane są punkty \(A=(1,1), B=(4,-2)\). Znajdź punkt \(C\), który jest wierzchołkiem trójkąta równobocznego \(ABC\).

Pokaż rozwiązanie zadania.

Zadanie nr 4.

Dany jest trójkąt równoboczny o boku \(a\). Środki boków tego trójkąta dzielą dany trójkąt na mniejsze części. Oblicz wysokość mniejszego trójkąta leżącego w środku danego trójkąta.

Pokaż rozwiązanie zadania.

Zadanie nr 5.

W trójkąt równoboczny o boku długości 2 wpisano kwadrat o polu 1. Oblicz wysokość trójkąta równoramiennego, wyznaczonego przez ten kwadrat.

Pokaż rozwiązanie zadania.

Zadanie nr 6.

Dany jest trójkąt równoboczny o boku a. Środki boków tego trójkąta dzielą dany trójkąt na mniejsze części. Wykaż, że wszystkie mniejsze trójkąty są przystające i są trójkątami równobocznymi.

Pokaż rozwiązanie zadania.

Zadanie nr 7 — maturalne.

Pole pewnego trójkąta równobocznego jest równe \(\frac{4\sqrt{3}}{9}\). Obwód tego trójkąta jest równy

A. 4

B. 2

C. \(\frac{4}{3}\)

D. 2/3

Pokaż rozwiązanie zadania.

Zadanie nr 8 — maturalne.

Wysokość trójkąta równobocznego jest równa \(6\sqrt{3}\). Pole tego trójkąta jest równe

A. \(3\sqrt{3}\)

B. \(4\sqrt{3}\)