Trójkąt prostokątny
Trójkąt prostokątny jest to trójkąt, w którym jeden z kątów jest kątem prostym. Każdy z boków, który leży przy tym kącie, nazywamy przyprostokątną, a bok leżący naprzeciw kąta prostego nazywamy przeciwprostokątną.
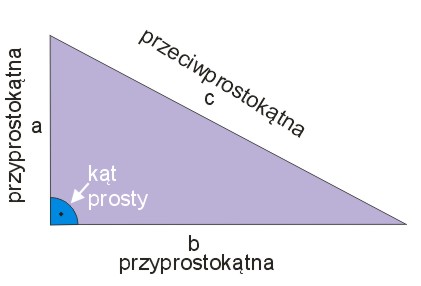
Wysokość w trójkącie prostokątnym
Trójkąt prostokątny ma tę cechę, że wysokość tego trójkąta stanowi przyprostokątna, jeżeli przyjąć za podstawę drugą przyprostokątną. Dzięki temu pole trójkąta prostokątnego wyjątkowo łatwo się liczy.
Pole trójkąta prostokątnego
Wzór na pole trójkąta prostokątnego o przyprostokątnych \(a\) i \(b\) jest następujący:
Własności trójkąta prostokątnego
Z trójkątem prostokątnym związanych jest bardzo dużo różnych twierdzeń. Część z nich omówimy tutaj, część w osobnych artykułach.
Twierdzenie Pitagorasa
Najbardziej znana własność trójkąta prostokątnego to twierdzenie Pitagorasa, któremu w niniejszym kursie został poświęcony osobny artykuł.
Przystawanie i podobieństwo
Twierdzenie 1
W trójkącie prostokątnym \(ABC\) wysokość \(\overline{CD}\) opuszczona z wierzchołka kąta prostego \(C\) na przeciwprostokątną \(\overline{AB}\) dzieli trójkąt na dwa trójkąty prostokątne \(ACD\) i \(CBD\) podobne do siebie i podobne do trójkąta \(ABC\).
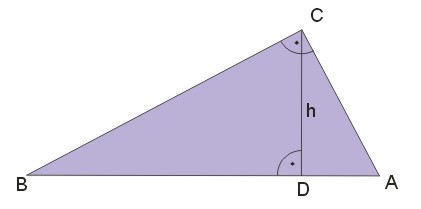
Twierdzenie 2 — Przystawanie trójkątów prostokątnych.
Jeżeli w dwóch trójkątach prostokątnych dwa boki jednego trójkąta są odpowiednio równe dwóm bokom drugiego trójkąta, a kąt prosty w jednym trójkącie jest położony względem tych boków tak samo, jak w drugim trójkącie, to trójkąty te są przystające.
Twierdzenie 3 — Podobieństwo trójkątów prostokątnych.
Jeżeli w dwóch trójkątach prostokątnych dwa boki jednego trójkąta są proporcjonalne do dwóch boków drugiego trójkąta, a kąt prosty w jednym trójkącie jest położony względem tych boków tak samo, jak w drugim trójkącie, to trójkąty te są podobne.
Inne właściwości
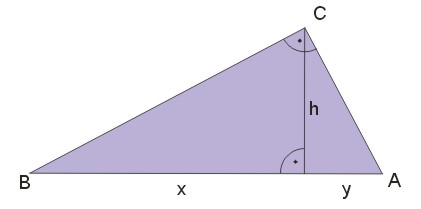
Twierdzenie 4
W trójkącie prostokątnym przyprostokątna wysokość opuszczona z wierzchołka kąta prostego na przeciwprostokątną dzieli ją na dwie części tak, że jest dla tych części średnią geometryczną \(h=\sqrt{x\cdot y}\).
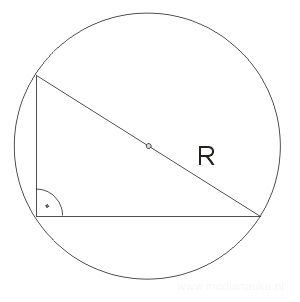
Okrąg opisany na trójkącie prostokątnym
Trójkąt oparty na średnicy jest prostokątny.
Trójkąt prostokątny równoramienny
Trójkąt prostokątny równoramienny to taki trójkąt prostokątny, którego ramiona mają równą długość. Kąty wewnętrzne mają miary 90°, 45° i 45°.
Przykład takiego trójkąta prostokątnego równoramiennego ilustruje poniższy rysunek.
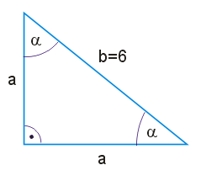
Wzór na długość przeciwprostokątnej w trójkącie równoramiennym prostokątnym: \(c=a\sqrt{2}\).
Wysokość w trójkącie równoramiennym prostokątnym to każda z przyprostokątnych oraz odcinek o długości połowy przeciwprostokątnej, czyli \(h=\frac{a\sqrt{a}}{2}\).
Pole powierzchni trójkąta prostokątnego równoramiennego to połowa pola kwadratu o boku długości a, czyli: \(P=\frac{a^2}{2}\).
Promień okręgu opisanego na trójkącie prostokątnym równoramiennym to połowa długości przeciwprostokątnej tego trójkąta, czyli \(R=\frac{a\sqrt{2}}{2}\).
Kąty w trójkącie prostokątnym
Jak w każdym trójkącie, suma kątów w trójkącie prostokątnym wynosi 180°. Ponieważ jeden z kątów ma miarę 90°, to suma pozostałych dwóch kątów zawsze jest równa 90°
Pytania
Dlaczego nie istnieje trójkąt prostokątny równoboczny?
W trójkącie prostokątnym jeden z kątów zgodnie z definicją trójkąta prostokątnego musi mieć 90°, a w trójkącie równobocznym prostokątnym wszystkie kąty wewnętrzne musiałyby mieć miarę 90° (zgodnie z własnościami trójkąta równobocznego). Suma kątów w każdym trójkącie jest równa 180°, a 3·90°=270°.
Jak sprawdzić, czy trójkąt jest prostokątny?
Jeżeli kwadrat długości boku trójkąta jest równy sumie kwadratów długości pozostałych boków, to trójkąt taki jest prostokątny (spełnia twierdzenie Pitagorasa).
Czym jest środkowa w trójkącie prostokątnym?
Przypomnijmy, że środkowa w trójkącie jest to odcinek łączący środek boku trójkąta z przeciwległym wierzchołkiem trójkąta. W przypadku trójkąta prostokątnego jest to zatem połowa przeciwprostokątnej, a jednocześnie promień okręgu opisanego na tym trójkącie. Warto dodać, że środek ciężkości w trójkącie prostokątnym konstruujemy analogicznie jak w każdym innym trójkącie (środkowe trzech boków trójkąta przecinają się w jednym punkcie).
Jak narysować okrąg wpisany w trójkąt równoboczny?
Dwusieczne kątów trójkąta prostokątnego przecinają się w jednym punkcie, który jest środkiem okręgu wpisanego w ten trójkąt.
Jak definiujemy funkcje trygonometryczne w trójkącie prostokątnym?
Tematowi temu poświęcono odrębny artykuł.
Zadania z rozwiązaniami

Zadanie nr 1.
Na trójkącie prostokątnym o przyprostokątnych długości 3 i 4 opisano koło. Oblicz pole i obwód tego koła.

Zadanie nr 2.
W trójkącie prostokątnym jeden z kątów wewnętrznych ma miarę 30°. Oblicz miarę pozostałych kątów w tym trójkącie.

Zadanie nr 3.
W trójkącie prostokątnym miary dwóch kątów wewnętrznych są równe, a długość przeciwprostokątnej jest równa 6. Oblicz miarę kątów w tym trójkącie oraz długość boków.

Zadanie nr 4.
W trójkącie prostokątnym długości przyprostokątnych wynoszą odpowiednio 5 i 8. Oblicz długość przeciwprostokątnej.

Zadanie nr 5.
W trójkącie prostokątnym wysokość o długości \(2\sqrt{2}\) opuszczona z wierzchołka kąta prostego dzieli podstawę na dwa odcinki, z których jeden jest dwa razy dłuższy od drugiego. Oblicz długości boków trójkąta.

Zadanie nr 6.
W równoramiennym trójkącie prostokątnym przyprostokątne mają długość 10 cm. Obliczyć długość promienia okręgu opisanego na tym trójkącie.

Zadanie nr 7.
Jaką długość mają przyprostokątne trójkąta prostokątnego, jeżeli wiadomo, że jedna z przyprostokątnych jest 3 razy dłuższa od drugiej i średnica okręgu opisanego na tym trójkącie ma długość równą \(\sqrt{10}\).

Zadanie nr 8.
Długość przeciwprostokątnej w trójkącie prostokątnym równoramiennym jest dwa razy większa od długości przyprostokątnej. Oblicz długości boków tego trójkąta.

Zadanie nr 9.
Znaleźć punkt na prostej \(y=1\), który wraz z punktami \(A=(2,3), B=(4,2)\) wyznaczy trójkąt prostokątny.

Zadanie nr 10 — maturalne.
Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta styczna do okręgu o promieniu 4 w punkcie \(P\) przechodzi przez środek okręgu o promieniu 3 (zobacz rysunek).
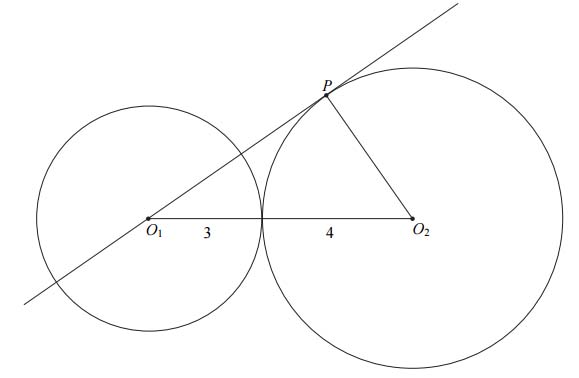
Pole trójkąta, którego wierzchołkami są środki okręgów i punkt styczności \(P\), jest równe:
A. \(14\)
B. \(2\sqrt{33}\)
C. \(4\sqrt{33}\)
D. \(12\)
Powiązane materiały
Ćwiczenia, sprawdziany i quizy
 Trójkąty prostokątne
Trójkąty prostokątne© medianauka.pl, 2010-12-04, A-1041
Data aktualizacji artykułu: 2023-06-15

 Trójkąt
Trójkąt Trójkąt równoboczny
Trójkąt równoboczny Twierdzenie Pitagorasa
Twierdzenie Pitagorasa Twierdzenia o trójkącie
Twierdzenia o trójkącie Pole trójkąta i obwód trójkąta
Pole trójkąta i obwód trójkąta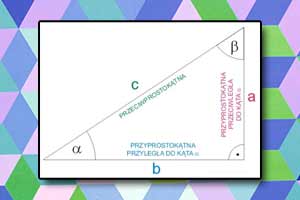 Funkcje trygonometryczne sinus cosinus tangens
Funkcje trygonometryczne sinus cosinus tangens Trójkąty
Trójkąty



