Nauka » Matematyka » Trójkąt prostokątny

Zadanie - trójkąt prostokątny

Treść zadania:

Znaleźć punkt na prostej $y=1$, który wraz z punktami $A=(2,3), B=(4,2)$ wyznaczy trójkąt prostokątny.

Rozwiązanie zadania

Możliwe są tutaj trzy różne przypadki. Oto jeden z nich:

Przypadek 1

Interesuje nas przypadek, w którym wierzchołkiem kąta prostego jest punkt $A$. Sporządzamy szkic.

Szukamy punktu $C$, który leży na prostej $y=1$, zatem jego współrzędna $y$ jest równa 1. Współrzędne szukanego punktu C oznaczamy:

$C=(x_1,1)$

Punkt $C$ leży na prostej prostopadłej do prostej, która jest wyznaczona przez punkty $A$ i $B$. Szukamy prostej wyznaczonej przez punkty $A$ i $B$, której równanie oznaczamy następująco: $y=ax+b$. Równanie tej prostej znajdziemy, podstawiając do kierunkowego równania prostej współrzędne punktów $A$ i $B$

$y=ax+b\\ A=(2,3), \ B=(4,2)\\ \underline{ \ - \ \begin{cases} 3=2a+b\\ 2=4a+b \end{cases}}\\ 1=-2a/:(-2)\\ a=-\frac{1}{2}\\ 2=4a+b\\ 2=4\cdot (-\frac{1}{2})+b\\ 2=-2+b\\ b=4\\ y=-\frac{1}{2}x+4$

Przy wyznaczeniu równania prostej wyznaczonej przez punkty $A$, $C$ skorzystamy z własności prostych prostopadłych. Współczynniki kierunkowe prostych prostopadłych spełniają warunek:

$a=-\frac{1}{a_1}$

Ponadto prosta ta przechodzi przez punkt $A$, którego współrzędne znamy, mamy więc:

$a_1=-\frac{1}{a}=-\frac{1}{-\frac{1}{2}}=2$

$y=a_1x+b_1$

$y=2x+b_1$

$A=(2,3)$

$3=2\cdot 2+b_1$

$b_1=-1$

$y=2x-1$

Punkt $C$ leży na tej prostej, więc podstawiamy współrzędne punktu $C$ do prostej wyżej wyznaczonej:

$C=(x_1,1)$

$y=2x-1$

$1=2x_1-1$

$2x_1=2/:2$

$x_1=1$

$C=(1,1)$

Przypadek 2

Interesuje nas przypadek, w którym wierzchołkiem kąta prostego jest punkt $B$ . Sporządzamy szkic.

Szukamy punktu $D$, który leży na prostej $y=1$, zatem jego współrzędna $y$ jest równa 1. Współrzędne szukanego punktu $D$ oznaczymy:

$D=(x_2,1)$

Punkt $D$ leży na prostej prostopadłej do prostej, która jest wyznaczona przez punkty $A$ i $B$, której równanie znaleźliśmy w rozpatrywanym przypadku 1.

Przy wyznaczeniu równania prostej wyznaczonej przez punkty $B$, $D$ skorzystamy z własności prostych prostopadłych. Współczynniki kierunkowe prostych prostopadłych spełniają warunek:

$a=-\frac{1}{a_1}$

Ponadto prosta ta przechodzi przez punkt $B$, którego współrzędne znamy, mamy więc:

$a_2=-\frac{1}{a}=-\frac{1}{-\frac{1}{2}}=2$

$y=a_2x+b_2$

$y=2x+b_2$

$B=(4,2)$

$2=4\cdot 2+b_2$

$b_2=-6$

$y=2x-6$

Punkt $D$ leży na tej prostej, więc podstawiamy współrzędne punktu $D$ do prostej wyżej wyznaczonej:

$D=(x_2,1)$

$y=2x-6$

$1=2x_2-6$

$2x_2=7/:2$

$x_2=\frac{7}{2}$

$C=(\frac{7}{2},1)$

Przypadek 3

Interesuje nas przypadek, w którym wierzchołkiem kąta prostego jest punkt $E$. Sporządzamy szkic.

Szukamy punktu $E$, który leży na prostej $y=1$, zatem jego współrzędna $y$ jest równa 1. Współrzędne szukanego punktu $E$ oznaczymy:

$E=(x_3,1)$

Szukamy prostej, wyznaczonej przez punkty $A$, $E$, podstawiając ich współrzędne do równania:

$y=a_3x+b_3\\ A=(2,3), \ E=(x_3,1)\\ \underline{ \ - \ \begin{cases} 3=a_3\cdot 2+b_3\\ 1=a_3\cdot x_3+b_3\end{cases}}\\ 2=2a_3-a_3x_3\\ 2=a_3(2-x_3)/:(2-x_3)\\ a_3=\frac{2}{2-x_3}, \ x_3\neq 2$

Ograniczymy się tylko do wyznaczenia współczynnika kierunkowego prostej, gdyż wartość $x_3$ znajdziemy z warunku dotyczącego współczynników kierunkowych prostych prostopadłych.

Szukamy prostej, wyznaczonej przez punkty $B$, $E$, podstawiając ich współrzędne do równania:

$y=a_4x+b_4\\ B=(4,2), \ E=(x_3,1)\\ \underline{ \ - \ \begin{cases} 2=a_4\cdot 4+b_4\\ 1=a_4\cdot x_3+b_4\end{cases}}\\ 1=4a_4-a_4x_3\\ 1=a_4(4-x_3)/:(4-x_3)\\ a_4=\frac{1}{4-x_3}, \ x_3\neq 4$

Skorzystamy z własności prostych prostopadłych. Współczynniki kierunkowe prostych prostopadłych spełniają warunek:

$a_3=-\frac{1}{a_4}$

Mamy więc:

$a_3=-\frac{1}{a_4}$

$\frac{2}{2-x_3}=-\frac{1}{\frac{1}{4-x_3}}$

$\frac{2}{2-x_3}=-(4-x_3)$

$\frac{2}{2-x_3}=x_3-4/\cdot (2-x_3), \ bo \ x_3\neq 2$

$2=(2-x_3)(x_3-4)$

$2=2x_3-8-x_3^2+4x_3$

$x_3^2-6x_3+10=0$

$\Delta=36-40=-4<0$

Ponieważ wyróżnik trójmianu kwadratowego jest ujemny, równanie nie ma rozwiązania, zatem rozpatrywane proste nie mogą tworzyć kąta prostego. Przypadek tu rozpatrywany nie zachodzi. Co jednak, gdy $x_3=2$ lub $x_3=4$? W obu przypadkach otrzymujemy punkty o współrzędnych $(2,1)$, $(4,1)$, które z punktami $A$ i $B$ tworzą proste prostopadłe do prostej o równaniu $y=1$. Nie zachodzi tutaj przypadek utworzenia z tych punktów wraz z $A$, $B$ trójkąta prostokątnego.

Odpowiedź

$C=(1,1), \ D=(\frac{7}{2},1)$

Matura z matematyki

Zbiór zadań maturalnych z ubiegłych lat na poziomie podstawowym i rozszerzonym oraz centrum dowodzenia dla maturzystów.

Zbiór zadań z matematyki

Zbiór zadań z matematyki wraz z pełnymi rozwiązaniami. W naszej bazie zgromadziliśmy ponad tysiąc zadań.

WYKRESY ONLINE

Narysuj wykres funkcji w programie do szkicowania wykresów i odczytaj jego własności.

Zadania podobne

Zadanie nr 1.

Na trójkącie prostokątnym o przyprostokątnych długości 3 i 4 opisano koło. Oblicz pole i obwód tego koła.

Pokaż rozwiązanie zadania.

Zadanie nr 2.

W trójkącie prostokątnym jeden z kątów wewnętrznych ma miarę 30°. Oblicz miarę pozostałych kątów w tym trójkącie.

Pokaż rozwiązanie zadania.

Zadanie nr 3.

W trójkącie prostokątnym miary dwóch kątów wewnętrznych są równe, a długość przeciwprostokątnej jest równa 6. Oblicz miarę kątów w tym trójkącie oraz długość boków.

Pokaż rozwiązanie zadania.

Zadanie nr 4.

W trójkącie prostokątnym długości przyprostokątnych wynoszą odpowiednio 5 i 8. Oblicz długość przeciwprostokątnej.

Pokaż rozwiązanie zadania.

Zadanie nr 5.

W trójkącie prostokątnym wysokość o długości $2\sqrt{2}$ opuszczona z wierzchołka kąta prostego dzieli podstawę na dwa odcinki, z których jeden jest dwa razy dłuższy od drugiego. Oblicz długości boków trójkąta.

Pokaż rozwiązanie zadania.

Zadanie nr 6.

W równoramiennym trójkącie prostokątnym przyprostokątne mają długość 10 cm. Obliczyć długość promienia okręgu opisanego na tym trójkącie.

Pokaż rozwiązanie zadania.

Zadanie nr 7.

Jaką długość mają przyprostokątne trójkąta prostokątnego, jeżeli wiadomo, że jedna z przyprostokątnych jest 3 razy dłuższa od drugiej i średnica okręgu opisanego na tym trójkącie ma długość równą $\sqrt{10}$.

Pokaż rozwiązanie zadania.

Zadanie nr 8.

Długość przeciwprostokątnej w trójkącie prostokątnym równoramiennym jest dwa razy większa od długości przyprostokątnej. Oblicz długości boków tego trójkąta.

Pokaż rozwiązanie zadania.

Zadanie nr 9 — maturalne.

Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta styczna do okręgu o promieniu 4 w punkcie $P$ przechodzi przez środek okręgu o promieniu 3 (zobacz rysunek).

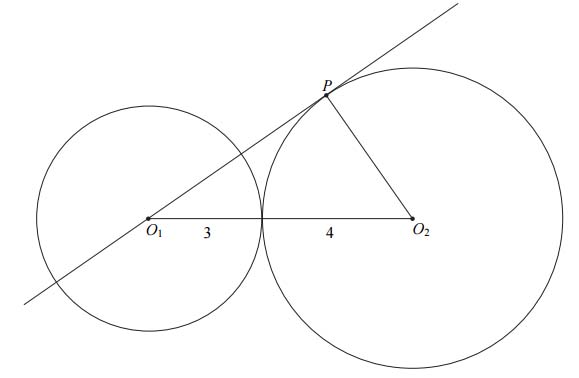
ilustracja do zadania

Pole trójkąta, którego wierzchołkami są środki okręgów i punkt styczności $P$, jest równe:

A. $14$

B. $2\sqrt{33}$

C. $4\sqrt{33}$

D. $12$

Pokaż rozwiązanie zadania.