Zadanie - trójkąt prostokątny
Treść zadania:
W trójkącie prostokątnym wysokość o długości \(2\sqrt{2}\) opuszczona z wierzchołka kąta prostego dzieli podstawę na dwa odcinki, z których jeden jest dwa razy dłuższy od drugiego. Oblicz długości boków trójkąta.
Rozwiązanie zadania
Sporządzamy szkic.
Wiemy z treści zadania, że jeden z odcinków podstawy jest dwa razy dłuższy od drugiego:
\(x=2y\)
W trójkącie prostokątnym wysokość opuszczona z wierzchołka kąta prostego na przeciwprostokątną dzieli ją na dwie części tak, że jest dla tych części średnią geometryczną:
\(h=\sqrt{xy}\)
\(h=2\sqrt{2}\)
\(2\sqrt{2}=\sqrt{2y\cdot y}\)
\(2\sqrt{2}=\sqrt{2y^2}\)
\(2\sqrt{2}=y\sqrt{2}/:\sqrt{2}\)
\(y=2\)
\(x=4\)
Możemy więc obliczyć długość podstawy:
\(c=x+y\)
\(c=2+4\)
\(c=6\)
Znając długości \(x\) oraz \(y\), możemy, korzystając z twierdzenia Pitagorasa, wyznaczyć długości \(a\) oraz \(b\), gdyż wysokość dzieli nasz trójkąt na dwa trójkąty prostokątne. Zatem zgodnie z twierdzeniem Pitagorasa w trójkącie prostokątnym kwadrat przeciwprostokątnej jest równy sumie kwadratów przyprostokątnych:
\(a^2=x^2+h^2\)
\(a^2=4^2+(2\sqrt{2})^2\)
\(a^2=16+4\cdot 2\)
\(a^2=24\)
\(a=\sqrt{24}=\sqrt{4\cdot 6}=2\sqrt{6}\)
Dla drugiego trójkąta:
\(b^2=y^2+h^2\)
\(b^2=2^2+(2\sqrt{2})^2\)
\(b^2=4+4\cdot 2\)
\(b^2=12\)
\(b=\sqrt{12}=\sqrt{4\cdot 3}=2\sqrt{3}\)
Odpowiedź
\(a=2\sqrt{6}, \ b=2\sqrt{3}, \ c=6\)© medianauka.pl, 2011-02-07, ZAD-1134


Zadania podobne
Zadanie nr 1.
Na trójkącie prostokątnym o przyprostokątnych długości 3 i 4 opisano koło. Oblicz pole i obwód tego koła.
Zadanie nr 2.
W trójkącie prostokątnym jeden z kątów wewnętrznych ma miarę 30°. Oblicz miarę pozostałych kątów w tym trójkącie.
Zadanie nr 3.
W trójkącie prostokątnym miary dwóch kątów wewnętrznych są równe, a długość przeciwprostokątnej jest równa 6. Oblicz miarę kątów w tym trójkącie oraz długość boków.
Zadanie nr 4.
W trójkącie prostokątnym długości przyprostokątnych wynoszą odpowiednio 5 i 8. Oblicz długość przeciwprostokątnej.
Zadanie nr 5.
W równoramiennym trójkącie prostokątnym przyprostokątne mają długość 10 cm. Obliczyć długość promienia okręgu opisanego na tym trójkącie.
Zadanie nr 6.
Jaką długość mają przyprostokątne trójkąta prostokątnego, jeżeli wiadomo, że jedna z przyprostokątnych jest 3 razy dłuższa od drugiej i średnica okręgu opisanego na tym trójkącie ma długość równą \(\sqrt{10}\).
Zadanie nr 7.
Długość przeciwprostokątnej w trójkącie prostokątnym równoramiennym jest dwa razy większa od długości przyprostokątnej. Oblicz długości boków tego trójkąta.
Zadanie nr 8.
Znaleźć punkt na prostej \(y=1\), który wraz z punktami \(A=(2,3), B=(4,2)\) wyznaczy trójkąt prostokątny.

Zadanie nr 9 — maturalne.
Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta styczna do okręgu o promieniu 4 w punkcie \(P\) przechodzi przez środek okręgu o promieniu 3 (zobacz rysunek).
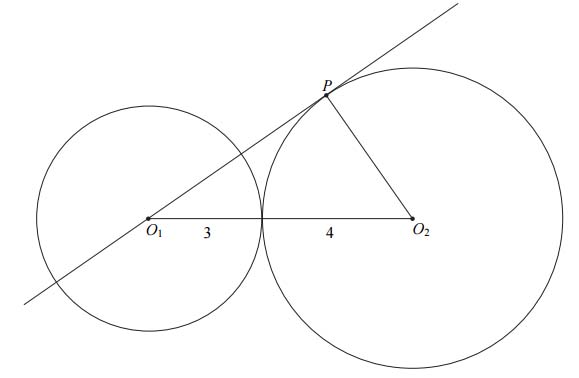
Pole trójkąta, którego wierzchołkami są środki okręgów i punkt styczności \(P\), jest równe:
A. \(14\)
B. \(2\sqrt{33}\)
C. \(4\sqrt{33}\)
D. \(12\)






