Objętość
Co to jest objętość brył? Oto definicja objętości:
Objętość figury jest to funkcja, która każdej figurze z pewnego zbioru figur przyporządkowuje liczbę nieujemną \(V(f)\), którą nazywamy objętością figury \(f\). Funkcja ta określona jest tak, że:
- Figury przystające mają przystające objętości.
- Figura będąca sumą dwóch figur, które nie mają wewnętrznych punktów wspólnych, ma objętość równą sumie objętości figur składowych.
Wzory na objętość brył
Jak obliczyć objętość danej figury geometrycznej przestrzennej? Najczęściej obliczanie objętości sprowadza się do zastosowania odpowiedniego wzoru. W poniższej tabeli zawarto podstawowe wzory na objętość brył:

Tablica objętości brył
Poniższa tabela zawiera wzory na objętość brył, najczęściej wykorzystywane w kursie matematyki.
| Bryła | Rysunek | Wzór na objętość |
| Sześcian | 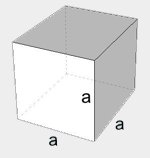 | \(V=a^3\) |
| Prostopadłościan | 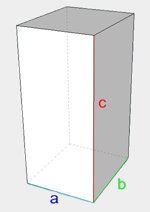 | \(V=abc\) |
| Dowolny graniastosłup prosty i pochyły | 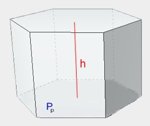 | \(V=P_p\cdot h\) \(P_p\) — pole podstawy, \(h\) — wysokość. |
| Czworościan foremny | 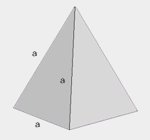 | \(V=\frac{1}{12}a^3\sqrt{2}\) |
| Dowolny ostrosłup prosty lub pochyły | 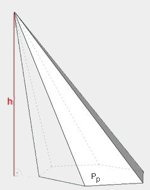 | \(V=\frac{1}{3}P_p\cdot h\) |
| Piramida | 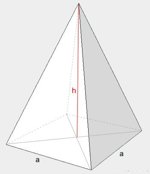 | \(V=\frac{a^2h}{3}\) |
| Ostrosłup ścięty | 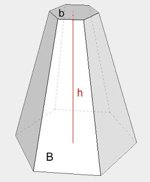 | \(V=\frac{1}{3}h(B+\sqrt{Bb}+b)\) |
| Ośmiościan foremny | 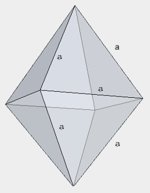 | \(V=\frac{1}{3}a^3\sqrt{2}\) |
| Dwunastościan foremny | 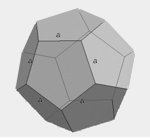 | \(V=\frac{1}{4}a^3(15+7\sqrt{5})\) |
| Dwudziestościan foremny |  | \(V=\frac{5}{12}a^3(3+\sqrt{5})\) |
| Walec | 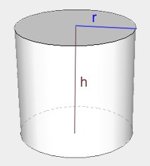 | \(V=\pi r^2h\) |
| Stożek | 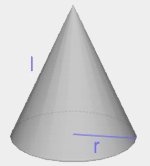 | \(V=\frac{1}{3}\pi r^2h\) |
| Kula | 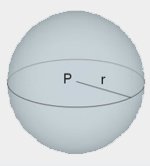 | \(V=\frac{4}{3}\pi r^3\) |
Jednostka objętości
Jeżeli odcinek \(\overline{u}\) jest jednostką długości, to sześcian o krawędzi \(\overline{u}\) nazywamy jednostką objętości i oznaczamy \(\overline{u}^3\).
Przykład
Jeżeli za jednostkę długości przyjmiemy metr (\(m\)), to jednostką objętości będzie metr sześcienny (\(m^3\)), jeżeli za jednostkę długości przyjmiemy decymetr (\(dm\)), to jednostką objętości będzie decymetr sześcienny (\(dm^3\)) itd.
Oto jednostki objętości dawne i obecnie stosowane.
Metr sześcienny
W układzie SI legalną jednostką objętości jest metr sześcienny (\(m^3\)). Stosując różne przedrostki, otrzymujemy centymetry sześcienne, decymetry sześcienne itd.
Litr
Pozaukładową jednostką jest litr, którą oznaczamy przez \(l\) (mała litera). Przelicznik litra na jednostki układu SI jest następujący:
Litr jest to objętość, jaką zajmuje 1 kg destylowanej wody w odpowiednich warunkach.
Anglosaskie jednostki objętości
W krajach anglosaskich stosuje się następujące jednostki objętości:
- cal sześcienny,
- stopa sześcienna,
- jard sześcienny.
Dawne miary objętości
Oto przykładowe dawne miary objętości:
- korzec — 128 litrów,
- kwaterka — \(\frac{1}{4}\) litra,
- kwarta — 1 litr.
Przeliczanie jednostek objętości
W naszym kalkulatorze możesz w prosty sposób przeliczyć dane objętości między różnymi układami jednostek.
Zasada Cavalierego
Jeżeli dwie bryły zawarte między dwoma równoległymi płaszczyznami mają własność, że ich przekroje dowolną płaszczyzną równoległą do poprzednich dwóch płaszczyzn mają równe pola, to bryły te mają równe objętości (patrz rysunek).
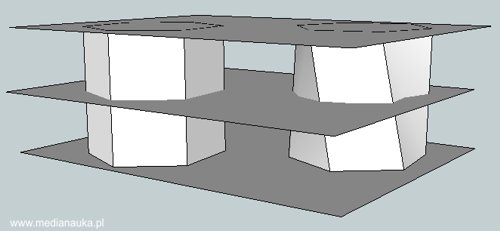
Własności objętości
- Każda figura płaska (zawarta w płaszczyźnie) ma objętość równą 0.
- Każda powierzchnia wielościanu ma objętość równą 0.
- Każda sfera i jej część ma objętość równą 0.
- Każda powierzchnia stożkowa i jej część ma objętość równą 0.
- Podobieństwo w skali \(s\) zmienia objętość figury w skali \(s^3\).
Ciekawostki — przykładowe objętości
W Poniższej tabeli wyszczególniono przykładowe wartości objętości.
| Objętość obiektu | V [\(m^3\)] |
|---|---|
| Wszechświat (obserwowalny) | Około \(10^{79}\) |
| Objętość Słońca | \(1,41\cdot 10^{27}\) |
| Objętość Ziemi | \(1,08\cdot 10^{21}\) |
| Objętość wieloryba | Maksymalnie \(200\) |
| Objętość płuc człowieka | \(0,003-0,007\) (\(3-7\) litrów) |
| Objętość ludzkiej krwi | \(0,0035-0,006\) (od \(3,5\) do \(6\) litrów) |
| Objętość komórki bakterii | \(10^{-18}-10^{-16}\) |
| Objętość jądra atomu tlenu | \(5\cdot 10^{-44}\) |
Zadania
Zadania z obliczania objętości znajdziesz w sekcji poświęconej poszczególnym bryłom.
Pytania
Jak obliczyć objętość?
Najczęściej korzystamy z powyższych wzorów. Jeżeli jednak bryłą ma skomplikowany kształt, spróbuj ją podzielić na bryły, których objętość można policzyć i dodaj do siebie tak wyznaczone objętości. W praktyce objętość bryły o nieregularnych kształtach można wyznaczyć, zanurzając ją w wodzie i obliczeniu objętości wypartej w ten sposób wody.
Jak obliczyć objętość prostokąta?
Prostokąt nie jest bryłą. Ma zerową objętość.
Wybrane karty pracy
Powiązane materiały
 Widok z góry
Widok z góry Ile kostek?
Ile kostek? Objętość — quiz
Objętość — quiz© medianauka.pl, 2011-08-09, A-1409
Data aktualizacji artykułu: 2023-07-01



 Bryła
Bryła Kąt dwuścienny i wielościenny
Kąt dwuścienny i wielościenny Proste prostopadłe w przestrzeni
Proste prostopadłe w przestrzeni Stereometria — podstawy
Stereometria — podstawy