Stereometria
Stereometria, geometria przestrzeni to dział geometrii, który bada figury geometryczne i związki między nimi w przestrzeni. Jest to geometria przestrzeni trójwymiarowej. Najczęściej odnosi się do geometrii euklidesowej. Znane są też ujęcia nieeuklidesowe. Inne przykłady geometrii przestrzennej to geometria przestrzeni hiperbolicznej i rzutowej.
TESTY I ZADANIA
Bryły
TESTY I ZADANIA
Aksjomaty stereometrii
Poniżej przedstawiamy aksjomaty dotyczące stereometrii:
Aksjomat XI o przestrzeni
W przestrzeni istnieje co najmniej jedna płaszczyzna, żadna płaszczyzna nie wypełnia całej przestrzeni, inaczej mówiąc: dla każdej płaszczyzny istnieje w przestrzeni co najmniej jeden punkt, który nie należy do tej płaszczyzny.
Aksjomat XII o płaszczyznach mających punkt wspólny.
Jeżeli dwie płaszczyzny mają punkt wspólny, to mają co najmniej jeszcze jeden punkt wspólny.
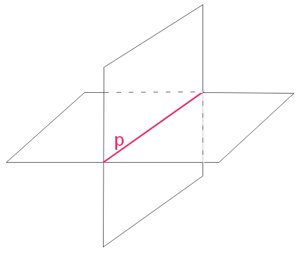
Aksjomat XIII o części wspólnej dwóch płaszczyzn.
Jeżeli dwie różne płaszczyzny mają punkt wspólny, to ich częścią wspólną jest prosta.
(patrz ilustracja obok)
Aksjomat XIV o płaszczyźnie przechodzącej przez trzy punkty.
Przez każde trzy punkty przechodzi co najmniej jedna płaszczyzna (punkty nie muszą być różne).
Wniosek z aksjomatów XIII i XIV - Przez trzy punkty niewspółliniowe przechodzi dokładnie jedna płaszczyzna.
Aksjomat XV
Każda płaszczyzna w przestrzeni ma wszystkie własności przyjęte z planimetrii (geometrii płaszczyzny).
Aksjomat XVI o odległości punktów w przestrzeni
Jeśli dwa punkty leżą na jednej płaszczyźnie i te same dwa punkty leżą na drugiej płaszczyźnie, to odległość między tymi punktami jest na każdej z tych płaszczyzn taka sama.
Inne wnioski z powyższych aksjomatów:
- Dwie proste przecinające się wyznaczają dokładnie jedną płaszczyznę.
- Prosta i punkt, który nie należy do tej prostej wyznaczają dokładnie jedną płaszczyznę.
© medianauka.pl, 2023-02-04, A-4679
Data aktualizacji artykułu: 2023-06-29

 Bryła
Bryła Kąt dwuścienny i wielościenny
Kąt dwuścienny i wielościenny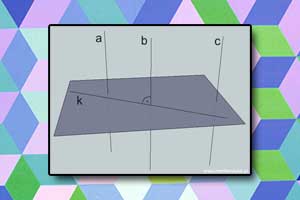 Proste prostopadłe w przestrzeni
Proste prostopadłe w przestrzeni Objętość
Objętość Wielościan
Wielościan Czworościan foremny
Czworościan foremny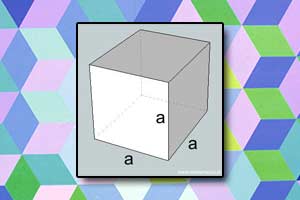 Sześcian
Sześcian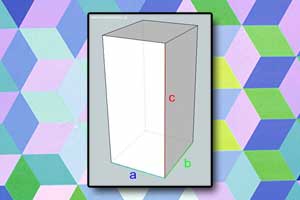 Prostopadłościan
Prostopadłościan Graniastosłup
Graniastosłup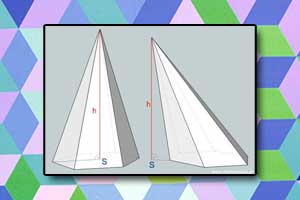 Ostrosłup
Ostrosłup Kula, sfera
Kula, sfera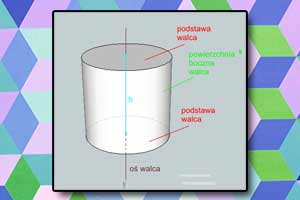 Walec
Walec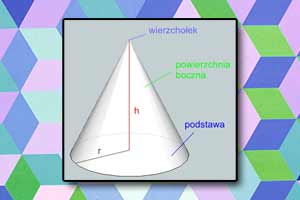 Stożek
Stożek