Kula

Kula o środku \(P\) i promieniu \(r\) jest to zbiór wszystkich punktów przestrzeni, których odległości od pewnego punktu \(P\) przestrzeni są nie większe od \(r\), gdzie \(r\) jest długością danego niezerowego odcinka \(\overline{r}\). Oznaczenie sfery jest następujące: \(K(P,r)\).

kula

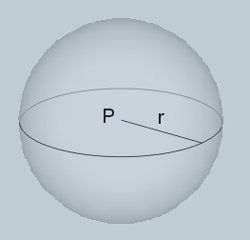
Kula powstaje przy obrocie koła wokół jego średnicy o kąt pełny.

Koło wielkie kuli

koło wielkie kuli

Jeżeli płaszczyzna przechodzi przez środek kuli (patrz rysunek), to przecina ją i w przekroju (pole zakreskowane) otrzymujemy koło o promieniu równym promieniowi kuli. Jest to koło wielkie tej kuli. Każdy inny przekrój kuli (gdy płaszczyzna nie przechodzi przez środek kuli) daje koło o mniejszym promieniu lub punkt, gdy płaszczyzna przechodzi przez punkt sfery. O takiej płaszczyźnie mówimy, że jest styczna do kuli (sfery), a przekrój nazywamy punktem styczności.

Sfera

Sfera (powierzchnia kulista) o środku \(P\) i promieniu \(r\) jest to zbiór wszystkich punktów przestrzeni, których odległości od pewnego punktu \(P\) przestrzeni są równe \(r\), gdzie \(r\) jest długością danego niezerowego odcinka \(\overline{r}\). Oznaczenie sfery jest następujące: \(S(P,r)\).

sfera

Dowolny punkt, który należy do sfery, nazywamy zwyczajnie punktem sfery. Środek sfery i promień nie należą do sfery. Odcinek łączący środek sfery z dowolnym punktem sfery jest promieniem tej sfery.

Sfera powstaje przy obrocie okręgu wokół jego średnicy o kąt pełny.

Sfera \(S(P,r)\) jest powierzchnią (brzegiem) kuli \(K(P,r)\). Promień tej sfery jest promieniem kuli. Średnicą kuli nazywamy odcinek, którego końce należą do sfery kuli i który przechodzi przez środek kuli.

Pole sfery

Pole sfery o promieniu \(R\) dane jest wzorem:

\(S=4\pi R^2\)

Pole sfery to nic innego jak pole powierzchni kuli.

Objętość kuli

Jak obliczyć objętość kuli? Oto wzór na objętość kuli.

Objętość kuli o promieniu \(R\) dana jest wzorem:

\(V=\frac{4}{3}\pi R^3\)

Widać, że istnieje związek między objętością kuli a polem sfery o tym samym promieniu. Wzór na objętość kuli możemy zapisać w następujący sposób:

\(V=S\cdot \frac{1}{3}R\)

Przykład

Dana jest kula o promieniu 3. Oblicz jej objętość i pole powierzchni.

\(V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi\cdot 3^3=4\pi \cdot 3^2=36\pi\)

\( S=4\pi R^2=4\pi \cdot 3^2=36\pi\)

Zauważ, że otrzymaliśmy ten sam wynik liczbowy. Czy zatem jest to prawidłowy wynik? Oczywiście, że tak. Obie liczby są równe. Inne są jednak jednostki, w jakich wyrażona jest objętość i pole powierzchni.

Pytania

Czy kula ziemska jest rzeczywiście kulą?

Nie, kula ziemska to elipsoida. Używając potocznego języka, elipsoida to nieco spłaszczona kula od strony obu biegunów. Kula ziemska to również wiele nieregularnych kształtów na jej powierzchni w postaci na przykład gór.

Ćwiczenia

Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.

ĆWICZENIA

Kula i sfera

Zadania z rozwiązaniami

Zadanie nr 1.

Obliczyć pole powierzchni i objętość kuli o średnicy 18 cm.

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Z trzech pełnych kul, każdej o promieniu 10 cm, przelano wodę do jednej kuli o promieniu 30 cm. W jakiej części większa kula zapełni się wodą?

Pokaż rozwiązanie zadania.

Zadanie nr 3 — maturalne.

Na rysunku przedstawiono bryłę zbudowaną z walca i półkuli. Wysokość walca jest równa \(r\) i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.

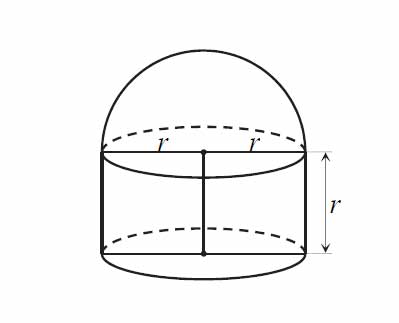
rysunek