Walec
Co to jest walec? Oto definicja walca.
Walec może być prosty lub pochyły.

Animacja
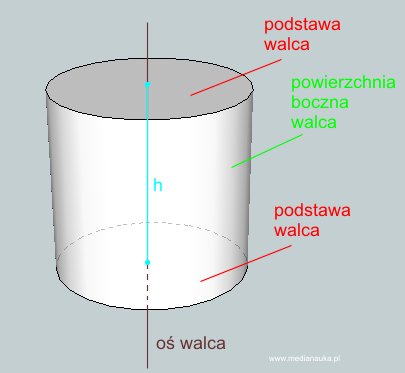
Poniższy rysunek opisuje takie pojęcia jak: wysokość \(h\) walca, oś walca, powierzchnia boczna i podstawa.
Objętość walca
Objętość walca jest równa iloczynowi pola podstawy walca (koła) przez wysokość walca. Wzór na objętość walca jest następujący:
Pole powierzchni walca
Pole powierzchni walca jest równe sumie pól podstaw walca (pole kół: \(\pi r^2+\pi r^2\)) i pola powierzchni bocznej \(P_b\) (pole prostokąta: \(2\pi r h\)). Wzory na pole powierzchni walca są następujące:
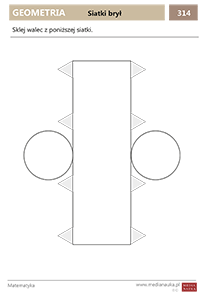
Siatka walca
Poniższy rysunek przedstawia siatkę walca. Przy sporządzaniu siatki walca (dla na przykład wykonania modelu bryły) pamiętać należy, że jeden z boków prostokąta ma długość równą wysokości walca, a drugi — równą obwodowi podstawy walca.
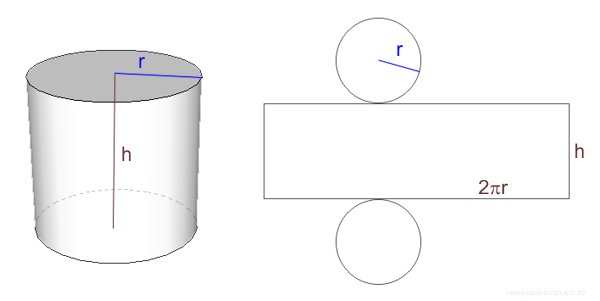
Jak zrobić walec z papieru? Na końcu artykułu zamieszczamy szablon w postaci karty pracy w formacie PDF siatki walca do druku.
Przekrój osiowy i poprzeczny walca
Każdy przekrój osiowy walca przechodzący przez jego oś jest prostokątem, którego długość jednego boku jest równa średnicy podstawy walca, a drugiego — wysokości walca. Natomiast przekrój poprzeczny walca płaszczyzną prostopadłą do osi walca jest kołem przystającym do podstawy.
Pytania
Jak obliczyć pojemność walca w litrach?
Pojemność walca to nic innego jak jego objętość. Stosujemy zatem wzór na objętość walca. Jeden litr to jeden decymetr sześcienny. Musimy zatem pamiętać o odpowiednim przeliczeniu jednostek.
Na przykład, aby obliczyć pojemność walca o wysokości \(h=0,1\ m\) i promieniu podstawy \(r=20\ cm\), wykonujemy przeliczenia:
\(h=0,1\ m=1\ dm\)
\(r=20\ cm=2\ dm\)
\(V=\pi r^2h=\pi(2\ dm)^2\cdot 1\ dm=2\pi \ dm^3=2\pi \ l \approx 6,28\ l\)
Zadania z rozwiązaniami

Zadanie nr 1.
Dany jest walec o wysokości 10 cm i promieniu podstawy 4 cm. Obliczyć jego objętość i pole powierzchni.

Zadanie nr 2.
Jaki promień podstawy musi mieć naczynie w kształcie walca o wysokości 30 cm, aby zmieścić w nim 3 litry mleka?

Zadanie nr 3 — maturalne.
Stożek i walec mają takie same podstawy i równe pola powierzchni bocznych. Wtedy tworząca stożka jest:
A. sześć razy dłuższa od wysokości walca.
B. trzy razy dłuższa od wysokości walca.
C. dwa razy dłuższa od wysokości walca.
D. równa wysokości walca.

Zadanie nr 4 — maturalne.
Na rysunku przedstawiono bryłę zbudowaną z walca i półkuli. Wysokość walca jest równa \(r\) i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.
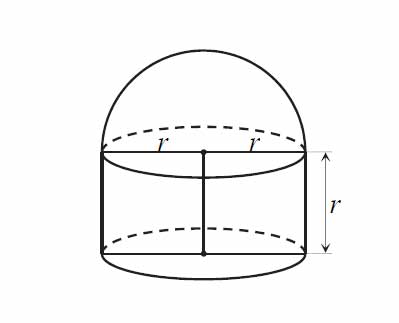
Objętość tej bryły jest równa
A. \(\frac{5}{3\pi r^3}\)
B. \(\frac{4}{3\pi r^3}\)
C. \(\frac{2}{3\pi r^3}\)
D. \(\frac{1}{3\pi r^3}\)

Zadanie nr 5 — maturalne.
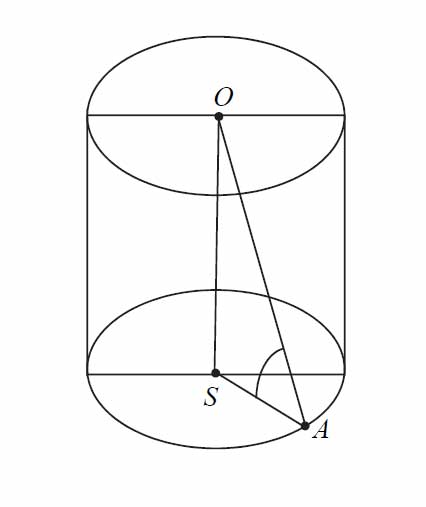
Promień \(AS\) podstawy walca jest równy połowie wysokości \(OS\) tego walca. Sinus kąta \(OAS\) (zobacz rysunek) jest równy
A. \(\frac{\sqrt{5}}{2}\)
B. \(\frac{2\sqrt{5}}{5}\)
C. \(\frac{1}{2}\)
D. \(1\)
Wybrane karty pracy
Powiązane materiały
© medianauka.pl, 2011-08-06, A-1406
Data aktualizacji artykułu: 2023-07-06


 Czworościan foremny
Czworościan foremny Stożek
Stożek figury obrotowe
figury obrotowe Dlaczego garnki są okrągłe?
Dlaczego garnki są okrągłe?