Zadanie - pole powierzchni i objętość walca

Dany jest walec o wysokości 10 cm i promieniu podstawy 4 cm. Obliczyć jego objętość i pole powierzchni.

Rozwiązanie zadania uproszczone

$V=\pi{r^2}\cdot{h}=\pi\cdot{(4\quad{cm}})^2\cdot{10\quad{cm}}=160\pi\quad{cm^3}$
$P=2\pi{r}(r+h)=2\pi\cdot(4cm)(4cm+10cm)=112\pi\quad{cm^2}$

Rozwiązanie zadania ze szczegółowymi wyjaśnieniami

Oznaczmy wysokość walca przez h=10 cm i promień podstawy przez r=4 cm.

Objętość walca obliczamy ze wzoru:

$V=\pi{r^2}\cdot{h}$

Obliczamy objętość walca, podstawiając dane do wzoru:

$V=\pi{r^2}\cdot{h}=\pi\cdot{(4\quad{cm}})^2\cdot{10\quad{cm}}=\pi\cdot{16\quad{cm}^2}\cdot{10\quad{cm}}=160\pi\quad{cm^3}$

Pole powierzchni walca obliczamy ze wzoru:

$P=2\pi{r}(r+h)$

Obliczamy pole powierzchni walca, podstawiając dane do wzoru:

$P=2\pi{r}(r+h)=2\pi\cdot(4cm)(4cm+10cm)=2\pi\cdot{4cm}\cdot{14cm}=112\pi\quad{cm^2}$

Odpowiedź

$V=160\pi{cm^3}\\P=112\pi{cm^2}$

Zadania podobne

Zadanie - objętość walca
Jaki promień podstawy musi mieć naczynie w kształcie walca o wysokości 30 cm, aby zmieścić w nim 3 litry mleka?

Pokaż rozwiązanie zadania

Zadanie maturalne nr 20, matura 2014
Stożek i walec mają takie same podstawy i równe pola powierzchni bocznych. Wtedy tworząca stożka jest:

A. sześć razy dłuższa od wysokości walca
B. trzy razy dłuższa od wysokości walca.
C. dwa razy dłuższa od wysokości walca.
D. równa wysokości walca.

Pokaż rozwiązanie zadania

Zadanie maturalne nr 22, matura 2018

Na rysunku przedstawiono bryłę zbudowaną z walca i półkuli. Wysokość walca jest równa r
i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.

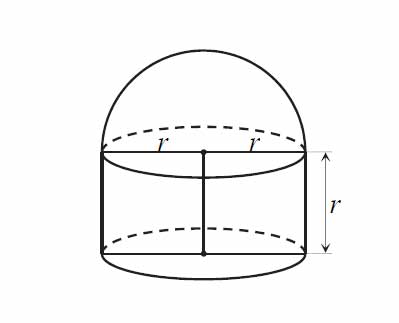
rysunek

Objętość tej bryły jest równa

5/3πr³
4/3πr³
2/3πr³
1/3πr³

Pokaż rozwiązanie zadania

Zadanie maturalne nr 21, matura 2019

Promień AS podstawy walca jest równy połowie wysokości OS tego walca. Sinus kąta OAS
(zobacz rysunek) jest równy

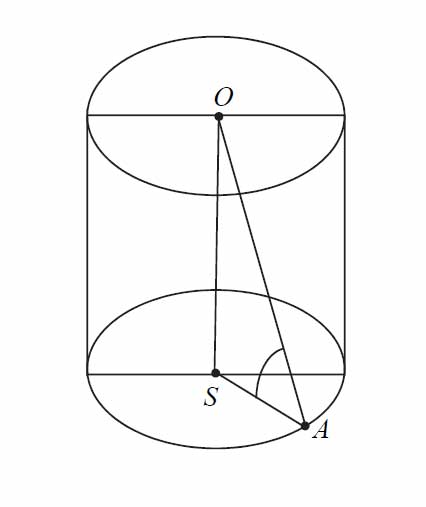
Rysunek

A. √5/2

B. 2√5/5

C. 1/2

D. 1

Pokaż rozwiązanie zadania

Niektóre treści nie są dostosowane do Twojego profilu. Jeżeli jesteś pełnoletni możesz wyrazić zgodę na przetwarzanie swoich danych osobowych. W ten sposób będziesz miał także wpływ na rozwój naszego serwisu.