Zadanie maturalne nr 21, matura 2019
Treść zadania:
Promień \(AS\) podstawy walca jest równy połowie wysokości \(OS\) tego walca. Sinus kąta \(OAS\) (zobacz rysunek) jest równy
A. \(\frac{\sqrt{5}}{2}\)
B. \(\frac{2\sqrt{5}}{5}\)
C. \(\frac{1}{2}\)
D. \(1\)
Rozwiązanie zadania
Oznaczmy przez |SA|=a. Wówczas zgodnie z warunkami zadania |OS|=2a. Aby obliczyć sunis kąta OAS musimy znać długośc przekątnej. Obliczymy ją z twierdzenia Pitagorasa dla trójkąta OSA:
\(a^2+(2a)^2=|OA|^2\)
\(5a^2=|OA|^2\)
\(|OA|=a\sqrt{5}\)
Zatem:
\(sin\angle\ OAS=\frac{|OS|}{|OA|})
\(sin\angle\ OAS=\frac{2a}{a\sqrt{5}}\)
\(sin\angle\ OAS=\frac{2\cdot \sqrt{5}}{\sqrt{5}\cdot \sqrt{5}}\)
\(sin\angle\ OAS=\frac{2\sqrt{5}}{5}\)
Odpowiedź
Odpowiedź B© medianauka.pl, 2023-01-31, ZAD-4667
Zadania podobne
Zadanie nr 1.
Dany jest trójkąt równoramienny o podstawie długości \(a\), ramionach długości \(b\), kątami wewnętrznymi przy podstawie trójkąta \(\beta\) oraz \(\alpha\) przy wierzchołku trójkąta z którego opada wysokość \(h\) na podstawę trójkąta. Zapisać podstawowe funkcje trygonometryczne dla katów: \(\beta, \frac{\alpha}{2}\).
Zadanie nr 2.
Dany jest trójkąt prostokątny równoramienny o przyprostokątnej długości \(a=\sqrt{2}\). Oblicz długość podstawy korzystając z funkcji trygonometrycznych.
Zadanie nr 3.
Obliczyć długość podstawy prostokąta, jeżeli przekątna o długości \(d=2\sqrt{3}\) tworzy z podstawą kąt \(\alpha=30°\).
Zadanie nr 4.
Obliczyć promień \(R\) okręgu opisanego na sześciokącie foremnym, jeżeli wiadomo, że długość promienia wpisanego w ten wielokąt \(r=2\).
Zadanie nr 5 — maturalne.
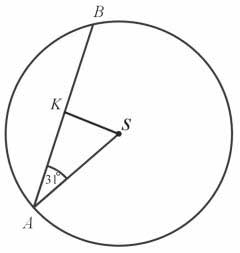W okręgu o środku w punkcie \(S\) poprowadzono cięciwę \(AB\), która utworzyła z promieniem \(AS\) kąt o mierze 31° (zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu \(S\) od cięciwy \(AB\) jest liczbą z przedziału
A. \(\langle \frac{9}{2};\frac{11}{2}\rangle\)
B. \(\langle \frac{11}{2};\frac{13}{2}\rangle\)
C. \(\langle \frac{13}{2};\frac{19}{2}\rangle\)
D. \(\langle \frac{19}{2};\frac{37}{2}\rangle\)
Zadanie nr 6 — maturalne.
Kąt \(\alpha\) jest ostry i \(tg{\alpha}=\frac{2}{3}\). Wtedy:
A. \(\sin{\alpha}=\frac{3\sqrt{13}}{26}\)
B. \(\sin{\alpha}=\frac{\sqrt{13}}{13}\)
C. \(\sin{\alpha}=\frac{2\sqrt{13}}{13}\)
D. \(\sin{\alpha}=\frac{3\sqrt{13}}{13}\)
Zadanie nr 7 — maturalne.
Kąt rozwarcia stożka ma miarę 120°, a tworzącą tego stożka ma długość 4. Objętość tego stożka jest równa
A. \(36\pi\)
B. \(18\pi\)
C. \(24\pi\)
D. \(8\pi\)
Zadanie nr 8 — maturalne.
Przekątna podstawy graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
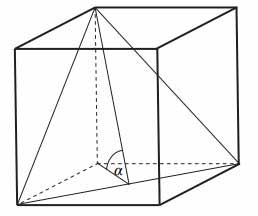
Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt α o mierze
A. 30°
B. 45°
C. 60°
D. 75°
Zadanie nr 9 — maturalne.
Tangens kąta \(\alpha\) zaznaczonego na rysunku jest równy:
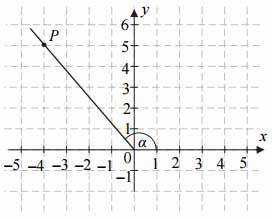
A. \(-\frac{\sqrt{3}}{3}\)
B. \(-\frac{4}{5}\)
C. \(-1\)
D. \(-\frac{5}{4}\)
Zadanie nr 10 — maturalne.
Przyprostokątna \(LM\) trójkąta prostokątnego \(KLM\) ma długość \(3\), a przeciwprostokątna \(KL\) ma długość \(8\) (zobacz rysunek).
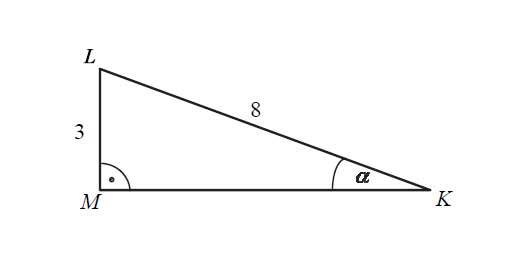
Wówczas miara α kąta ostrego LMK tego trójkąta spełnia warunek
- 27°<α≤30°
- 24°<α≤27°
- 21°<α≤24°
- 18°<α≤21°
Zadanie nr 11 — maturalne.
Sinus kąta ostrego \(\alpha\) jest równy \(\frac{4}{5}\). Wtedy
A. \(\cos{\alpha}=\frac{5}{6}\)
B. \(\cos{\alpha}=\frac{1}{5}\)
C. \(\cos{\alpha}=\frac{9}{25}\)
D. \(\cos{\alpha}=\frac{3}{5}\)
Zadanie nr 12 — maturalne.
Dany jest trójkąt prostokątny o kątach ostrych \(\alpha\) i \(\beta\) (zobacz rysunek).
Wyrażenie \(2\cos{\alpha}−\sin{\beta}\) jest równe
A. \(2\sin{\beta}\)
B. \(\cos{\alpha}\)
C. \(0\)
D. \(2\)