Stożek
Co to jest stożek? Oto definicja stożka:
Stożek może być prosty lub pochyły.

Animacja
Poniższy rysunek opisuje takie pojęcia jak: wysokość \(h\) stożka, powierzchnia boczna i podstawa.
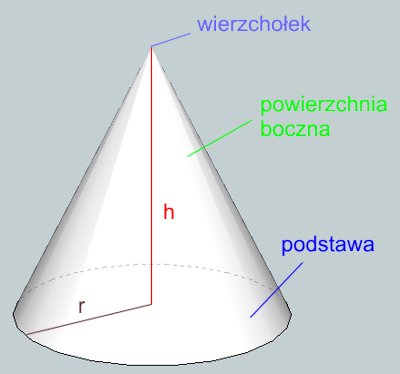
Objętość stożka
Jak obliczyć objętość stożka? Objętość stożka (prostego i pochyłego) jest równa jednej trzeciej iloczynu pola podstawy (koła) przez wysokość stożka. Wzór na objętość stożka jest następujący:
Pole powierzchni stożka
Pole powierzchni stożka jest równe sumie pól podstawy stożka (pole koła: \(\pi r^2\)) i pola powierzchni bocznej \(P_b\) (pole wycinka kołowego: \(\pi r l\)). Wzór na pole powierzchni stożka jest następujący:
Siatka stożka
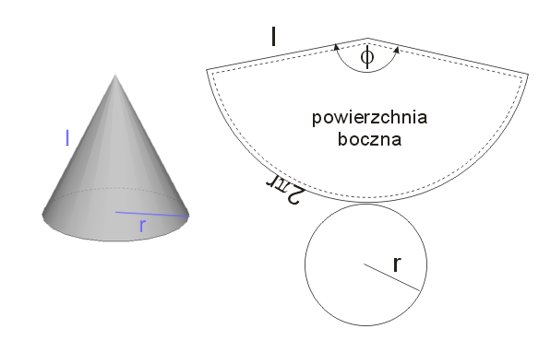
Poniższy rysunek przedstawia siatkę stożka. Przy sporządzaniu siatki stożka (dla na przykład wykonania modelu bryły) pamiętać należy, że dla narysowania powierzchni bocznej po rozwinięciu należy nakreślić koło o promieniu równym tworzącej \(l\) stożka, a z tego koła wyciąć wycinek o łuku równym obwodowi podstawy stożka. Aby to zrobić, należy posłużyć się proporcją: \(\phi :360=(2\pi r):(2 \pi l)\).
Przekrój osiowy i poprzeczny stożka
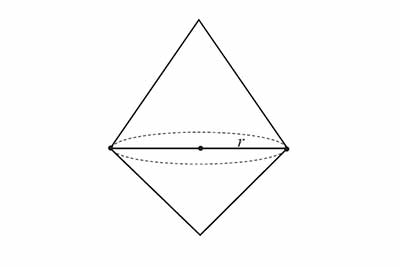
Każdy przekrój osiowy stożka przechodzący przez jego oś jest trójkątem równoramiennym, którego długość jednego boku jest równa średnicy podstawy stożka. Natomiast przekrój poprzeczny stożka płaszczyzną prostopadłą do osi stożka jest kołem.
Pytania
Jak zrobić stożek z papieru?
Stożek można wykonać z papieru (kartonu) na podstawie siatki stożka (przykładowa siatka została przedstawiona poniżej w formie karty pracy w formacie PDF). Siatkę należy wyciąć i skleić.
Co to jest tworząca stożka?
Tworząca stożka to odcinek łączący dowolny punkt na okręgu podstawy stożka z jego wierzchołkiem.
Co to jest kąt rozwarcia stożka?
Kąt rozwarcia stożka jest to kąt zawarty między bokami o długościach \(l\) w przekroju osiowym stożka.
Zadania z rozwiązaniami

Zadanie nr 1.
Dany jest stożek o promieniu podstawy 2 cm i wysokości 6 cm. Oblicz jego objętość i pole powierzchni.

Zadanie nr 2 — maturalne.
Kąt rozwarcia stożka ma miarę 120°, a tworzącą tego stożka ma długość 4. Objętość tego stożka jest równa
A. \(36\pi\)
B. \(18\pi\)
C. \(24\pi\)
D. \(8\pi\)

Zadanie nr 3 — maturalne.
Przekrojem osiowym stożka jest trójkąt równoboczny o boku długości 6 . Objętość tego stożka jest równa:
A. \(27\pi \sqrt{3}\)
B. \(9\pi \sqrt{3}\)
C. \(18\pi\)
D. \(6\pi\)

Zadanie nr 4 — maturalne.
Rozpatrujemy wszystkie stożki, których przekrojem osiowym jest trójkąt o obwodzie 20. Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.

Zadanie nr 5 — maturalne.
Dwa stożki o takich samych podstawach połączono podstawami w taki sposób jak na rysunku. Stosunek wysokości tych stożków jest równy 3:2 . Objętość stożka o krótszej wysokości jest równa 12 cm3 .
Objętość bryły utworzonej z połączonych stożków jest równa
A. 20 cm3
B. 30 cm3
C. 39 cm3
D. 52,5 cm3
Wybrane karty pracy
Powiązane materiały
© medianauka.pl, 2011-08-06, A-1407
Data aktualizacji artykułu: 2023-07-07


 Czworościan foremny
Czworościan foremny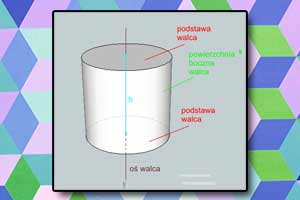 Walec
Walec figury obrotowe
figury obrotowe