Graniastosłup

Co to jest graniastosłup? Oto definicja graniastosłupa:

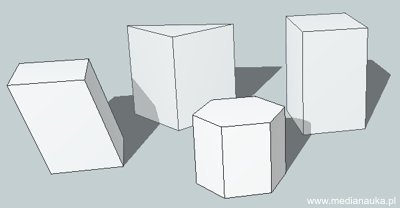
Graniastosłup jest to wielościan, którego wszystkie wierzchołki leżą na dwóch płaszczyznach równoległych (płaszczyznach podstaw dolnej i górnej), a którego wszystkie krawędzie nieleżące na tych płaszczyznach (tzw. krawędzie boczne) są równoległe.

graniastosłupy

Własności graniastosłupa

Z definicji wynika, że podstawy dolna i górna graniastosłupa są figurami płaskimi równoległymi i przystającymi o bokach także równoległych. Krawędzie graniastosłupa są równe. Ściany boczne są równoległobokami.

Ile wierzchołków ma graniastosłup?

Jeżeli graniastosłup w podstawie ma N-kąt, to taki graniastosłup ma 2N wierzchołków i 3N krawędzi oraz N+2 ścian.

Wysokość graniastosłupa

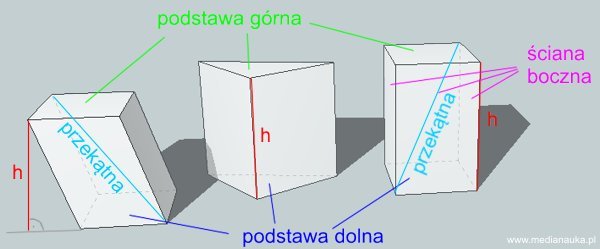
Wysokość graniastosłupa \(h\) jest to odcinek prostopadły do płaszczyzny podstaw, zawarty między tymi płaszczyznami o długości równej odległości płaszczyzn podstaw.

Przekątna graniastosłupa

Przekątna graniastosłupa jest to odcinek, który łączy dwa wierzchołki nieleżące na jednej ścianie.

przekątna graniastosłupa

Rodzaje graniastosłupów

Ze względu na podstawę rozróżniamy między innymi następujące graniastosłupy:

Graniastosłup trójkątny to taki graniastosłup, którego podstawą jest trójkąt.
Graniastosłup czworokątny to taki graniastosłup, którego podstawą jest czworokąt. Do tego rodzaju graniastosłupów zaliczamy sześcian i prostopadłościan, równoległościan.
Graniastosłup pięciokątny to taki graniastosłup, którego podstawą jest pięciokąt.
Graniastosłup sześciokątny to taki graniastosłup, którego podstawą jest sześciokąt.

Graniastosłup pochyły

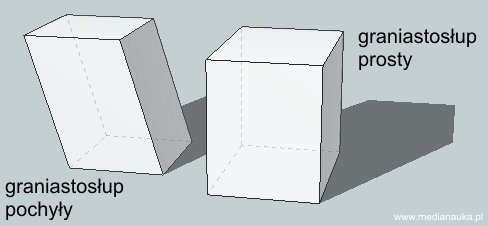
Graniastosłup pochyły to taki graniastosłup, którego krawędzie boczne nie są prostopadłe do podstaw.

Graniastosłup prosty

Graniastosłup prosty to taki graniastosłup, którego krawędzie boczne są prostopadłe do podstaw.

graniastosłup prosty i pochyły

Graniastosłup prawidłowy

Graniastosłup prawidłowy to graniastosłup prosty, którego podstawą jest wielokąt foremny (trójkąt równoboczny, kwadrat, pięciokąt foremny itd.).

Pozostałe rodzaje graniastosłupów:

Równoległościan — graniastosłup o podstawie będącej równoległobokiem.
Prostopadłościan — równoległościan, którego ściany są prostokątami.
Sześcian — prostopadłościan, którego wszystkie krawędzie są równe.
Graniastosłup prawidłowy czworokątny — to szczególny przypadek prostopadłościanu, którego podstawą jest kwadrat.

Objętość graniastosłupa

Jak obliczyć objętość graniastosłupa? Objętość dowolnego graniastosłupa (prostego lub pochyłego) jest równa iloczynowi pola podstawy przez wysokość.

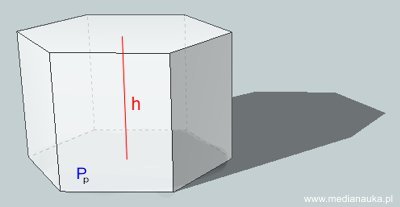
Objętość graniastosłupa

Wzór na objętość graniastosłupa jest następujący:

\(V=P_p\cdot h\)

Pole powierzchni graniastosłupa

Jak obliczyć pole powierzchni graniastosłupa? Pole powierzchni dowolnego graniastosłupa jest równe sumie pola powierzchni podstaw \(P_p\) oraz pola powierzchni bocznej (powierzchni ścian) tego graniastosłupa (\(P_b\)).

Wzór na pole powierzchni graniastosłupa jest następujący:

\(P=2P_p+P_b\)

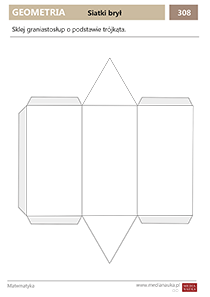
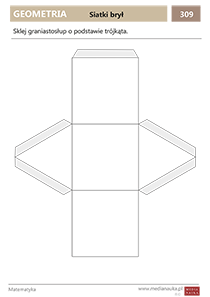
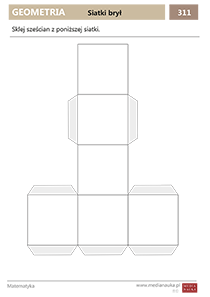
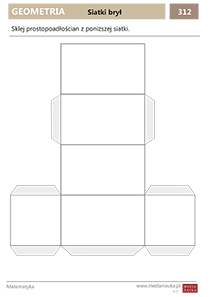
Siatka graniastosłupa

Jak zrobić graniastosłup z papieru? Gotowe szablony siatki graniastosłupa do druku i sklejenia znajdziesz na końcu artykułu w formacie PDF w formie karty pracy. Są to siatki graniastosłupów prostych.

Pytania

Ile krawędzi ma graniastosłup o 10 wierzchołkach?

Graniastosłup o 10 wierzchołkach ma w podstawie pięciokąty. Pięciokąt ma 5 krawędzi. Podstawy są dwie. Podstawy łączy ze sobą również 5 krawędzi bocznych. Zatem graniastosłup o 10 wierzchołkach ma 15 krawędzi.

Jak obliczyć pole boczne graniastosłupa?

Ściany boczne w graniastosłupie są zawsze równoległobokami. Jeżeli mamy dane krawędzie podstawy i wysokość, pole powierzchni bocznej obliczymy, sumując pola wszystkich pól. Warto dodać, że pole równoległoboku obliczamy ze wzoru \(P=ah\), gdzie \(h\) jest także wysokością graniastosłupa.

Jeżeli mamy do czynienia z graniastosłupem prawidłowym, pole powierzchni bocznej obliczymy, znając jedną z krawędzi podstawy a, mnożymy ją przez wysokość graniastosłupa i liczbę ścian bocznych.

Ile ścian ma graniastosłup prosty o N krawędziach?

Graniastosłup o \(N\) krawędziach ma \(\frac{N}{3}\) wierzchołków w podstawie. Zatem liczba ścian składa się z dwóch podstaw i \(\frac{N}{3}\) ścian bocznych.

Na przykład graniastosłup o 51 krawędziach ma 17-kąt w podstawie, a liczba ścian = 2 podstawy + 17 ścian bocznych = 19 ścian.

Ćwiczenia

Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.

ĆWICZENIA

Graniastosłupy

Zadania z rozwiązaniami

Zadanie nr 1 — maturalne.

Przekątna podstawy graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).

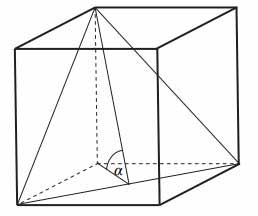
Ilustracja do zadania nr 24, matura z matematyki 2016, poziom podstawowy

Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt α o mierze

A. 30°

B. 45°

C. 60°

D. 75°

Pokaż rozwiązanie zadania.

Zadanie nr 2 — maturalne.

W graniastosłupie prawidłowym czworokątnym \(EFGHIJKL\) wierzchołki \(E, G, L\) połączono odcinkami (tak jak na rysunku).

wzór

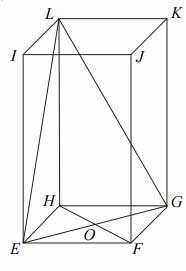
Wskaż kąt między wysokością \(OL\) trójkąta \(EGL\) i płaszczyzną podstawy tego graniastosłupa.

A. \(\angle HOL\)

B. \(\angle OGL\)

C. \(\angle HLO\)

D. \(\angle OHL\)

Pokaż rozwiązanie zadania.

Zadanie nr 3 — maturalne.

Każda krawędź graniastosłupa prawidłowego trójkątnego ma długość równą 8 . Pole powierzchni całkowitej tego graniastosłupa jest równe:

A. \(\frac{8^2}{3}(\frac{\sqrt{3}}{2}+3)\)

B. \(8^2\cdot \sqrt{3}\)

C. \(\frac{8^2\sqrt{6}}{3}\)

D. \(8^2(\frac{\sqrt{3}}{2}+3)\)

Pokaż rozwiązanie zadania.

Zadanie nr 4 — maturalne.

Wysokość graniastosłupa prawidłowego czworokątnego jest równa 16. Przekątna graniastosłupa jest nachylona do płaszczyzny jego podstawy, pod kątem którego cosinus jest równy 3/5. Oblicz pole powierzchni całkowitej tego graniastosłupa.

Pokaż rozwiązanie zadania.

Zadanie nr 5 — maturalne.

Dany jest graniastosłup prawidłowy trójkątny (zobacz rysunek). Pole powierzchni całkowitej tego graniastosłupa jest równe \(45\sqrt{3}\). Pole podstawy graniastosłupa jest równe polu jednej ściany bocznej. Oblicz objętość tego graniastosłupa.

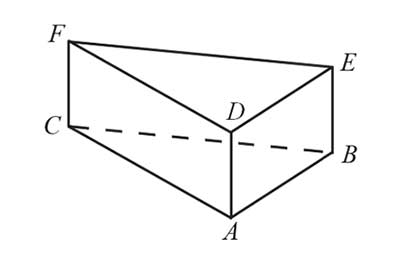
rysunek

Pokaż rozwiązanie zadania.

Zadanie nr 6 — maturalne.

Podstawą graniastosłupa prostego jest romb o przekątnych długości 7 cm i 10 cm. Wysokość tego graniastosłupa jest krótsza od dłuższej przekątnej rombu o 2 cm. Wtedy objętość graniastosłupa jest równa

A. \(560\ cm^3\)

B. \(280\ cm^3\)

C. \(\frac{280}{3} cm^3\)

D. \(\frac{560}{3} cm^3\)

Pokaż rozwiązanie zadania.

Zadanie nr 7 — maturalne.

Dany jest graniastosłup prosty \(ABCDEFGH\) o podstawie prostokątnej \(ABCD\). Przekątne \(AH\) i \(AF\) ścian bocznych tworzą kąt ostry o mierze \(\alpha\) takiej, że \(\sin{\alpha}=\frac{12}{13}\) (zobacz rysunek). Pole trójkąta \(AFH\) jest równe 26,4. Oblicz wysokość \(h\) tego graniastosłupa.

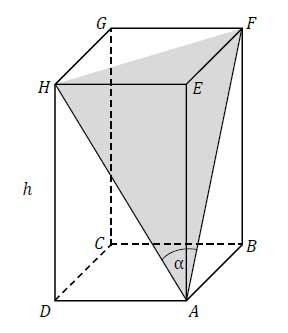
Matura 2022, zadanie 13

Pokaż rozwiązanie zadania.

Zadanie nr 8 — maturalne.

Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 15. Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem \(\alpha\) takim, że \(\cos{\alpha}=\frac{\sqrt{2}}{3}\). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Długość przekątnej tego graniastosłupa jest równa

A. \(15\sqrt{2}\)

B. \(45\)

C. \(5\sqrt{2}\)

D. \(10\)

Pokaż rozwiązanie zadania.