
Zadanie maturalne nr 13, matura 2022 - poziom rozszerzony
Treść zadania:
Dany jest graniastosłup prosty \(ABCDEFGH\) o podstawie prostokątnej \(ABCD\). Przekątne \(AH\) i \(AF\) ścian bocznych tworzą kąt ostry o mierze \(\alpha\) takiej, że \(\sin{\alpha}=\frac{12}{13}\) (zobacz rysunek). Pole trójkąta \(AFH\) jest równe 26,4. Oblicz wysokość \(h\) tego graniastosłupa.
Rozwiązanie zadania
Na rysunku wprowadzamy dodatkowe oznaczenia.
Dane jest pole trójkąta AFH. Skorzystajmy ze wzoru na pole trójkata:
\(P=\frac{1}{2}ab\sin{\gamma}\), gdzie \(a, b\) są długościami boków trójkąta, a \(\gamma\) jest kątem między tymi bokami.
\(P_{AFH}=\frac{1}{2}d\cdot e\cdot \sin{\alpha}\)
\(26.4=\frac{1}{2}d\cdot e\cdot \frac{12}{13}\)
\(d\cdot e=57,2\)
Dla tegoż tójkąta zastosujmy twierdzenie cosinusów:
\(c^2=d^2+e^2-2de\cos{\alpha}\)
\(c^2=d^2+e^2-2\cdot 57,2\cdot \cos{\alpha}\)
Korzystając z jedynki trygonometrycznej:
\(\cos^2{\alpha}=1-\sin^2{\alpha}=1-(\frac{12}{13})^2-\frac{25}{169}\)
Kat \(\alpha\) jest katem ostrym, więc \(\cos{\alpha}=\sqrt{\frac{25}{169}}=\frac{5}{13}\).
Mamy więc
\(c^2=d^2+e^2-2\cdot 57,2\cdot \frac{5}{13}\)
\(c^2=d^2+e^2-44\)
Korzystając z twierdzenia Pitagorasa:
\(c^2=a^2+b^2\)
\(d^2=h^2+a^2\)
\(e^2=h^2+b^2\)
mamy:
\(a^2+b^2=h^2+a^2+h^2+b^2-44\)
\(0=2h^2-44\)
\(h^2=22\)
\(h=\sqrt{22}\)
© medianauka.pl, 2023-04-29, ZAD-4891


Zadania podobne

Zadanie nr 1 — maturalne.
Przekątna podstawy graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
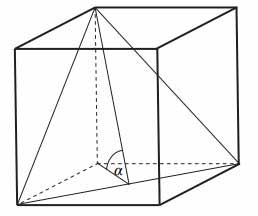
Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt α o mierze
A. 30°
B. 45°
C. 60°
D. 75°

Zadanie nr 2 — maturalne.
W graniastosłupie prawidłowym czworokątnym \(EFGHIJKL\) wierzchołki \(E, G, L\) połączono odcinkami (tak jak na rysunku).
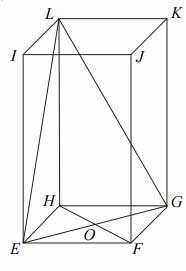
Wskaż kąt między wysokością \(OL\) trójkąta \(EGL\) i płaszczyzną podstawy tego graniastosłupa.
A. \(\angle HOL\)
B. \(\angle OGL\)
C. \(\angle HLO\)
D. \(\angle OHL\)

Zadanie nr 3 — maturalne.
Każda krawędź graniastosłupa prawidłowego trójkątnego ma długość równą 8 . Pole powierzchni całkowitej tego graniastosłupa jest równe:
A. \(\frac{8^2}{3}(\frac{\sqrt{3}}{2}+3)\)
B. \(8^2\cdot \sqrt{3}\)
C. \(\frac{8^2\sqrt{6}}{3}\)
D. \(8^2(\frac{\sqrt{3}}{2}+3)\)

Zadanie nr 4 — maturalne.
Wysokość graniastosłupa prawidłowego czworokątnego jest równa 16. Przekątna graniastosłupa jest nachylona do płaszczyzny jego podstawy, pod kątem którego cosinus jest równy 3/5. Oblicz pole powierzchni całkowitej tego graniastosłupa.

Zadanie nr 5 — maturalne.
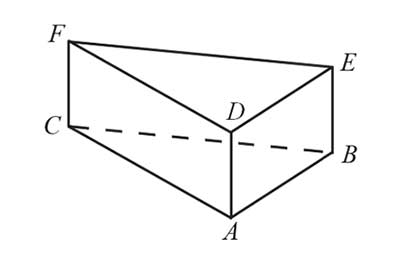
Dany jest graniastosłup prawidłowy trójkątny (zobacz rysunek). Pole powierzchni całkowitej tego graniastosłupa jest równe \(45\sqrt{3}\). Pole podstawy graniastosłupa jest równe polu jednej ściany bocznej. Oblicz objętość tego graniastosłupa.

Zadanie nr 6 — maturalne.
Podstawą graniastosłupa prostego jest romb o przekątnych długości 7 cm i 10 cm. Wysokość tego graniastosłupa jest krótsza od dłuższej przekątnej rombu o 2 cm. Wtedy objętość graniastosłupa jest równa
A. \(560\ cm^3\)
B. \(280\ cm^3\)
C. \(\frac{280}{3} cm^3\)
D. \(\frac{560}{3} cm^3\)

Zadanie nr 7 — maturalne.
Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 15. Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem \(\alpha\) takim, że \(\cos{\alpha}=\frac{\sqrt{2}}{3}\). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Długość przekątnej tego graniastosłupa jest równa
A. \(15\sqrt{2}\)
B. \(45\)
C. \(5\sqrt{2}\)
D. \(10\)

