Prostopadłościan

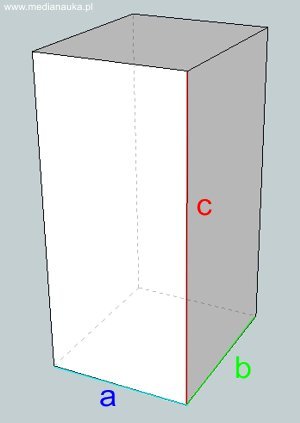
Prostopadłościan jest to graniastosłup, którego podstawy i ściany są prostokątami.

Objętość prostopadłościanu

Jak obliczyć objętość prostopadłościanu? Prostopadłościan jest graniastosłupem, a objętość graniastosłupa obliczamy, mnożąc pole powierzchni podstawy (prostokąta) przez wysokość (długość krawędzi bocznej). Wzór na objętość prostopadłościanu jest następujący:

V = a b c

Pole powierzchni prostopadłościanu

Jak obliczyć pole powierzchni całkowitej prostopadłościanu? Prostopadłościan jest graniastosłupem, a pole powierzchni graniastosłupa obliczamy, dodając pola powierzchni podstawy i pola powierzchni ścian bocznych. Wzór na pole powierzchni prostopadłościanu jest następujący:

P = 2 a b + 2 a c + 2 b c

Szczególnym przypadkiem prostopadłościanu jest sześcian.

Własności prostopadłościanu

Oto wybrane cechy każdego prostopadłościanu:

Wszystkie przekątne prostopadłościanu mają taka samą długość.
Przekątne prostopadłościanu przecinają się w środku symetrii tej bryły.
Wysokość prostopadłościanu jest równa długości jego krawędzi.

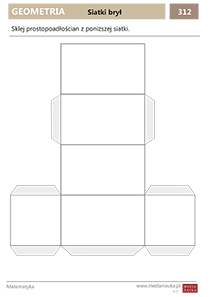
Jak wygląda siatka prostopadłościanu?

Siatkę prostopadłościanu przedstawia poniższa ilustracja.

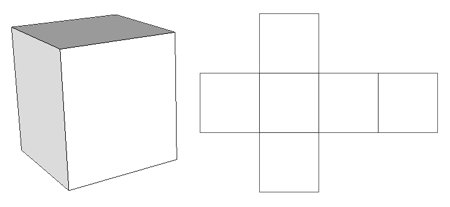
siatka sześcianu

Jak zrobić prostopadłościan z papieru? Gotowy szablon siatki prostopadłościanu do druku i sklejenia znajdziesz na końcu artykułu w formacie PDF w formie karty pracy.

Pytania

Jak obliczyć przekątną prostopadłościanu?

Przekątna p tworzy z krawędzią boczną i przekątną podstawy przeciwprostokątną w trójkącie prostokątnym. Na podstawie twierdzenia Pitagorasa można obliczyć: $p^{2} = a^{2} + b^{2} + c^{2}$ .

Czy sześcian jest prostopadłościanem?

Tak, każdy sześcian jest prostopadłościanem, ale nie każdy prostopadłościan jest sześcianem.

Ile krawędzi ma prostopadłościan?

Prostopadłościan ma 12 krawędzi.

Ile wierzchołków ma prostopadłościan?

Prostopadłościan ma 8 wierzchołków.

Co jest podstawą prostopadłościanu?

Każdy prostopadłościan ma sześć ścian. Wszystkie są prostokątami. Dwie z tych ścian nazywamy podstawami, pozostałe to ściany boczne. Boki prostokątów, które są ścianami prostopadłościanu, nazywamy krawędziami.

Jaki jest wzór na wysokość prostopadłościanu?

Wysokość prostopadłościanu o krawędziach $a, b, c$ to po prostu jedna z jego krawędzi. Jeżeli podstawa ma boki o długości $a$ i $b$ , to $c$ jest wysokością tego prostopadłościanu.

Zadania z rozwiązaniami

Zadanie nr 1 — maturalne.

Pole powierzchni całkowitej prostopadłościanu jest równe 198. Stosunki długości krawędzi prostopadłościanu wychodzących z tego samego wierzchołka prostopadłościanu to $1 : 2 : 3$ . Oblicz długość przekątnej tego prostopadłościanu.

Pokaż rozwiązanie zadania.

Zadanie nr 2 — maturalne.

Przekątne sąsiednich ścian bocznych prostopadłościanu wychodzące z jednego wierzchołka tworzą z jego podstawą kąty o miarach $\frac{π}{3}$ i $α$ . Cosinus kąta między tymi przekątnymi jest równy $\frac{\sqrt{6}}{4}$ . Wyznacz miarę kąta $α$ .

Pokaż rozwiązanie zadania.

Zadanie nr 3 — maturalne.

Podstawą graniastosłupa prostego jest prostokąt o bokach długości 3 i 4. Kąt α , jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy 45° (zobacz rysunek).

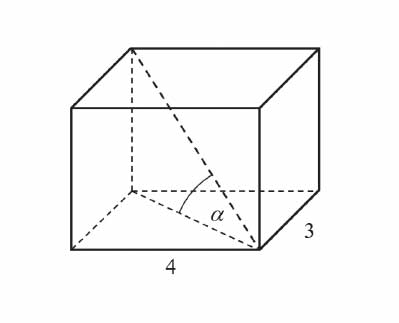
rysunek