
Zadanie maturalne nr 32, matura 2014
Treść zadania:
Pole powierzchni całkowitej prostopadłościanu jest równe 198. Stosunki długości krawędzi prostopadłościanu wychodzących z tego samego wierzchołka prostopadłościanu to \(1:2:3\). Oblicz długość przekątnej tego prostopadłościanu.
Rozwiązanie zadania
Przyjmijmy oznaczenia takie jak na poniższym rysunku:
Obliczamy pole powierzchni tego prostopadłościanu
\(P=2xy+2xz+2yz\)
Z założenia zadania \(1:2:3\) możemy uzyskać:
\(y=2x, z=3x\)
Podstawiamy powyższe zależności do wzoru na pole powierzchni:
\(P=2x\cdot 2x+2x\cdot 3x+2\cdot 2x\cdot 3z=4x^2+6x^2+12x^2=22x^2\)
z warunków zadania wiemy, że \(P=198\). Stąd:
\(22x^2=198/:22\)
\(x^2=9\)
\(x=3\)
\(y=2x=6\)
\(z=3x=9\)
Obliczamy długość przekątnej podstawy \(p\) z twierdzenia Pitagorasa:
\(p^2=x^2+y^2\)
\(p=\sqrt{x^2+y^2}\)
\(p=\sqrt{3^2+6^2}=\sqrt{9+36}=\sqrt{45}=3\sqrt{5}\)
Z tego samego twierdzenia obliczymy długość przekątnej \(d\):
\(d^2=p^2+z^2\)
\(d=\sqrt{p^2+z^2}\\)
\(d=\sqrt{(3\sqrt{5})^2+9^2}=\sqrt{9(5+9)}=3\sqrt{14}\)
Odpowiedź
\(d=3\sqrt{14}\)© medianauka.pl, 2017-02-05, ZAD-3455


Zadania podobne

Zadanie nr 1 — maturalne.
Przekątne sąsiednich ścian bocznych prostopadłościanu wychodzące z jednego wierzchołka tworzą z jego podstawą kąty o miarach \(\frac{\pi}{3}\) i \(\alpha\). Cosinus kąta między tymi przekątnymi jest równy \(\frac{\sqrt{6}}{4}\). Wyznacz miarę kąta \(\alpha\).

Zadanie nr 2 — maturalne.
Podstawą graniastosłupa prostego jest prostokąt o bokach długości 3 i 4. Kąt α , jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy 45° (zobacz rysunek).
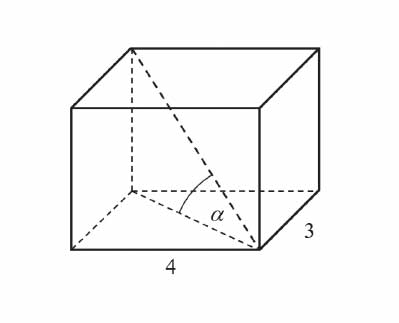
Wysokość graniastosłupa jest równa
- \(5\)
- \(3\sqrt{2}\)
- \(5\sqrt{2}\)
- \(\frac{5\sqrt{3}}{3}\)

