Miara kąta

Definicja

Każdemu kątowi przypisujemy pewną liczbę, zwaną miarą kąta, która spełnia następujące warunki:

kąt zerowy ma miarę 0,
kąt niezerowy ma miarę dodatnią,
miara sumy kątów równa jest sumie miar kątów,
miara kąta prostego jest dowolną, z góry ustaloną liczbą.

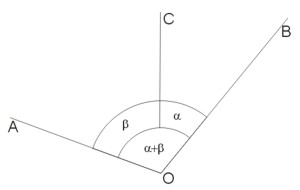
W definicji miary kąta jest mowa o sumie kątów. Jeżeli dwa kąty mają wspólne ramię i wierzchołek, ale ich wnętrza są rozłączne, to można utworzyć kąt, który nazwiemy sumą kątów, a którego obszarem jest suma obszarów danych kątów i którego wierzchołek jest wspólny tych kątów. Sumą tych kątów będziemy także nazywać każdy kąt przystający do nich. Jeżeli dwa kąty nie mają wspólnego wierzchołka i ramienia, to wówczas sumę tych kątów tworzymy tak, że przy jednym z ramion kąta odkładamy kąt przystający do drugiego kąta.

Miara stopniowa

Najczęściej posługujemy się miarą stopniową kąta. W mierze stopniowej kątowi prostemu przypisujemy liczbę 90, a kąt, którego miara jest równa 1 nazywamy stopniem i oznaczamy następująco: 1°.

Jeżeli dany jest kąt $\angle{ABC}$ , to jego miarę oznaczamy następująco: $|\angle{ABC}|$ . Jeżeli dany jest kąt $\angle{}\alpha$ , to jego miarę oznaczamy następująco: α

Kąt	miara
zerowy	0°
jednostkowy	1°
prosty	90°
półpełny	180°
pełny	360°

Kąt ostry jest to kąt o mierze stopniowej mniejszej niż 90°.

Kąt rozwarty jest to kąt o mierze stopniowej większej niż 90° i mniejszej niż 180°.

Jeden stopień miary stopniowej kąta dzieli się na 60 minut (oznaczenie: 60'), a każda minuta dzieli się na 60 sekund (oznaczenie: 60 '').

Posługujemy się także inną - miarą łukową kąta.

Miara łukowa kąta

Dany jest dowolny kąt nieskierowany na płaszczyźnie oraz okrąg o promieniu r i środku w wierzchołku tego kąta. Częścią wspólną tego okręgu i obszaru kąta jest łuk l.

Definicja

Łukowa miara kąta = $\frac{l}{r}$

Nie ma znaczenia, jaki promień zatoczymy z wierzchołka kąta. Miara łukowa dla danego kąta jest zawsze taka sama.

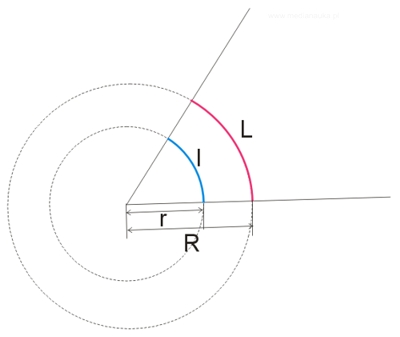
Dla kąta przedstawionego na rysunku mamy więc:

$\frac{l}{r}=\frac{L}{R}$

Radian

Definicja

Radian jest to kąt, którego miara łukowa jest równa 1.

Zatem inaczej mówiąc radian jest to kąt, w którym długość łuku jest równa długości promienia.

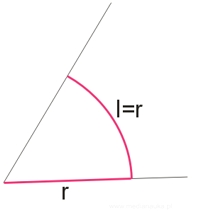
Jeden radian oznaczamy czasem symbolem rad, jednak możemy ten zapis pomijać, gdyż wymiar miary łukowej kąta to cm/cm.

Twierdzenie

Kąt pełny ma miarę łukową $2\pi$ .

$2\pi\ rad=360^o$

$1\ rad=\frac{360^o}{2\pi}=57^o17'45''$

Poniżej przedstawiamy sposób, w jaki obliczamy miarę łukową dowolnego kąta.

Kąt pełny ma miarę łukową równą $2\pi$ .
Miara łukowa kąta jest proporcjonalna do kąta.

Przykład

Dany jest kąt 45°. Wyznaczymy jego miarę łukową:

Układamy proporcję:

$360^o\ - \ 2\pi\\45^o - x$

$360^o\cdot x = 2\pi\cdot 45^o/:360^o\\ x=\frac{2\cdot 45^o}{360^o}\pi\\ x=\frac{90^o}{360^o}\pi\\ x=\frac{1}{4}\pi\\ x=\frac{\pi}{4}$

Przykład

Dany jest kąt $\frac{\pi}{3}$ . Wyznaczymy jego miarę stopniową:

Układamy proporcję:

$360^o\ - \ 2\pi\\x - \frac{\pi}{3}$

$360^o\cdot \frac{\pi}{3}=2\pi\cdot x/:2\pi\\ \frac{360^o \cdot \pi}{3\cdot 2\pi}\\ x= \frac{180^o}{3}\\ x=60^o$

Poniższa tabela zawiera miary najczęściej spotykanych kątów:

Miara stopniowa	Miara łukowa
360^o	$2\pi$
270^o	$\frac{3}{2}\pi$
180^o	$\pi$
90^o	$\frac{\pi}{2}$
60^o	$\frac{\pi}{3}$
45^o	$\frac{\pi}{4}$
30^o	$\frac{\pi}{6}$
1^o	$\frac{\pi}{180}$
1'	$\frac{\pi}{180\cdot 60}$
1''	$\frac{\pi}{180\cdot 60\cdot 60}$

Kalkulator
Przeliczanie miar kątów

Wpisz dane:

Zamień:

Miara kąta:

rad

Dokładność: miejsc po przecinku

Rozwiązanie:

Korzystamy z następującej zależności:
equation

Po przekształceniu otrzymujemy wzór:
equation

i korzystając z niego obliczamy:
equation

Korzystamy z następującej zależności:
equation

Po przekształceniu otrzymujemy wzór: equation

i korzystając z niego obliczamy: equation

Objaśnienia:

Miara kąta w radianach może być liczbą rzeczywistą lub wyrażeniem zawierającym podstawowe operatory matematyczne +, -, *, / oraz stałą PI.
Jeżeli wynik wskaże wartość "infinity" to oznacza, że jest poza zakresem dostępnym dla niniejszego kalkulatora.
Zapis wyniku 1.2e+12 oznacza liczbę 1.2 pomnożoną przez 10¹².
Gdy jedna z liczb będąca wynikiem działań jest większa od jej reprezentacji 64-bitowej, kalkulator stosuje przybliżenia wyniku.

Oprogramowanie: Natalia Okoń

Zadania z rozwiązaniami

Zadanie nr 1.

Dany jest kąt 85^o57'36''. Znaleźć jego miarę łukową.

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Wyrazić w stopniach, minutach i sekundach kąt 23,255^o.

Pokaż rozwiązanie zadania.

Zadanie nr 3.

Dany jest kąt $\frac{\pi}{8}\ rad$ . Znaleźć jego miarę stopniową. Wynik wyrazić w stopniach i minutach.

Pokaż rozwiązanie zadania.

Inne zagadnienia z tej lekcji

Kąt

Definicja kąta oraz opis różnych rodzajów kąta, w tym: kąta wypukłego, wklęsłego, środkowego, wpisanego w okrąg, kątów przyległych i wierzchołkowych.

Kąt skierowany

Kąt nieskierowany jest to zbiór utworzony z dwóch różnych półprostych o wspólnym początku i jednej z figur, wyciętych z płaszczyzny przez te dwie półproste.