Deltoid
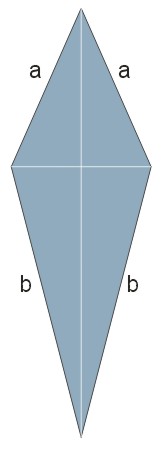
Deltoid jest to czworokąt, którego dwa kolejne boki są równe i dwa kolejne boki są równe między sobą, ale różne od poprzednich.
Deltoid to figura geometryczna, która przypomina latawiec.
Własności deltoidu
Oto wybrane twierdzenia związane z deltoidem:
- Dwa kąty zawarte między parami nierównych boków deltoidu są równe, pozostałe kąty nie są równe.
- Przekątne deltoidu są prostopadłe.
- Tylko jedna z przekątnych deltoidu jest dwusieczną dwóch kątów i symetralną drugiej przekątnej.
Pole deltoidu
Jak obliczyć pole deltoidu? Pole jest wyrażone za pomocą jego przekątnych. Wzór jest następujący:
Wzór na pole deltoidu o przekątnych \(d_1, d_2\) jest następujący:
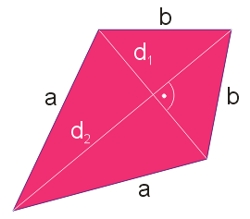
Obwód deltoidu
Obwód deltoidu wyraża się wzorem:
Wielkości \(a, b\) są długościami boków deltoidu.
Pytania
Jaki jest wzór na pole deltoidu na podstawie danych długości boków deltoidu?
Jeżeli \(a\) i \(b\) to długości boków deltoidu, a \(\phi\) to miara kąta między tymi bokami, to wzór na pole powierzchni deltoidu jest następujący: \(P=ab\sin{\phi}\).
Czy deltoid jest równoległobokiem albo rombem?
Nie, ponieważ żadne z dwóch boków nie są do siebie równoległe.
Ile boków ma deltoid?
Deltoid ma 4 boki.
Zadania z rozwiązaniami

Zadanie nr 1.
Z dwóch listewek o długości 30 cm i 1,2 m oraz kawałka materiału zbudowano latawiec w kształcie deltoidu tak, że listewki tworzą jego przekątne. Jakie jest pole powierzchni użytego materiału?

Zadanie nr 2 — maturalne.
Punkty \(A=(30,32)\) i \(B=(0,8)\) są sąsiednimi wierzchołkami czworokąta \(ABCD \) wpisanego w okrąg. Prosta o równaniu \(x-y+2=0\) jest jedyną osią symetrii tego czworokąta i zawiera przekątną \(AC\). Oblicz współrzędne wierzchołków \(C\) i \(D\) tego czworokąta.
Powiązane materiały
© medianauka.pl, 2010-11-26, A-1029
Data aktualizacji artykułu: 2023-06-28

 Trapez
Trapez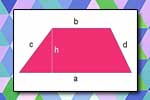 Pole i obwód trapezu
Pole i obwód trapezu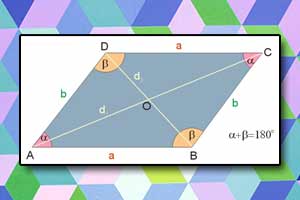 Równoległobok
Równoległobok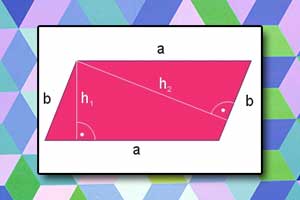 Pole równoległoboku
Pole równoległoboku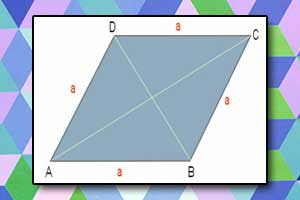 Romb
Romb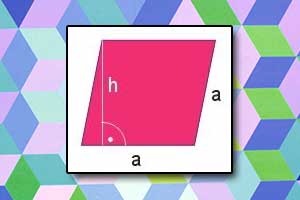 Pole rombu
Pole rombu Inne czworokąty
Inne czworokąty