Nauka » Matematyka » Figura geometryczna

Zadanie - działania na figurach geometrycznych

Treść zadania:

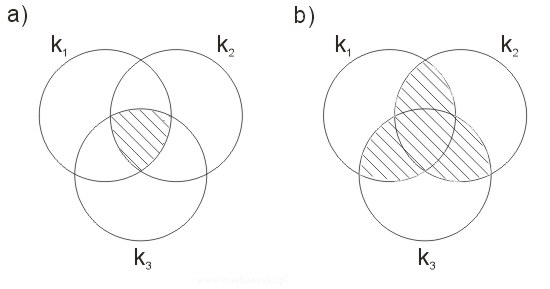
Opisać za pomocą działań na zbiorach część zakreskowaną kół $k_1, k_2, k_3$:

figury

Rozwiązanie zadania uproszczone

a) $k_1\cap k_2\cap k_3$
b) $(k_1\cap k_2\)\cup (k_2\cap k_3)\cup (k_1\cap k_3)$

a) Zauważamy, że zakreskowana figura jest częścią wspólną wszystkich kół (iloczynem trzech zbiorów - figur).

Zatem:

$k_1\cap k_2\cap k_3$

b) Zauważamy, że jeżeli dodamy do siebie części wspólne każdej pary kół, to otrzymamy szukaną (zakreskowaną) figurę.

Mamy więc:

$(k_1\cap k_2\)\cup (k_2\cap k_3)\cup (k_1\cap k_3)$

Matura z matematyki

Zbiór zadań maturalnych z ubiegłych lat na poziomie podstawowym i rozszerzonym oraz centrum dowodzenia dla maturzystów.

Zbiór zadań z matematyki

Zbiór zadań z matematyki wraz z pełnymi rozwiązaniami. W naszej bazie zgromadziliśmy ponad tysiąc zadań.

WYKRESY ONLINE

Narysuj wykres funkcji w programie do szkicowania wykresów i odczytaj jego własności.

Zadanie nr 1.

Dane są dowolne proste $a$ i $b$. Określić figury $a\cup b, \ a\cap b, \ a\setminus b, \ b\setminus a$.

Zadanie nr 2.

Dany jest okrąg $k$ i prosta $p$ przechodząca przez środek okręgu. Opisać figury: $k\cup p, \ k\cap p, \ k\setminus p, \ p\setminus k$.

Zadanie nr 3.

Dane są dwa trójkąty $t_1$ i $t_2$ usytuowane względem siebie tak, jak pokazuje rysunek.

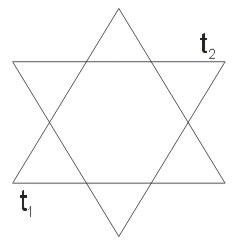
gwiazda

Zakreskować figury:

a) $t_1\cup t_2$

b) $t_1\cap t_2$

c) $t_1\setminus t_2$

d) $t_1\setminus t_2$

e) $(t_1\setminus t_2)\cup (t_2\setminus t_1)$

Zadanie nr 4.

Ile maksymalnie prostych może wyznaczyć 10 punktów na płaszczyźnie? A ile w przestrzeni?