Nauka » Matematyka » Figura geometryczna

Zadanie - figury geometryczne

Treść zadania:

Ile maksymalnie prostych może wyznaczyć 10 punktów na płaszczyźnie? A ile w przestrzeni?

Rozwiązanie zadania

Liczbę wyznaczonych prostych przez 10 punktów, z których każde 3 nie są współliniowe możemy policzyć, korzystając z pojęcia kombinacji k-elementowych zbioru n-elementowego. Dlaczego każde trzy mają być niewspółliniowe? Otóż, jeżeli dowolne trzy punkty będą współliniowe, to te trzy punkty wyznaczą dwie proste identyczne. W treści zadania szukamy maksymalnej liczby prostych, a więc nie interesują nas przypadki, w których proste są identyczne.

Mamy więc zbiór 10-elementowy punktów. Wybieramy dwa dowolne punkty, które zgodnie z aksjomatem o dwóch punktach i prostej wyznaczają jedną prostą (wybieramy 2 elementy ze zbioru 10-punktów, czyli \(k=2\)). Kolejność wyboru punktów nie ma znaczenia, bo czy wybierzemy punkt A, potem B, czy też najpierw B, a potem A, to i tak tworzymy jedną prostą między nimi. Punkty są różne i nie mogą się powtarzać (musimy wybierać 2 różne punkty), więc tworzymy kombinacje dwuelementowe zbioru 10-elementowego. (Spójrz na tabelę, w której zestawiono permutacje, kombinacje i wariacje.) Liczbę kombinacji oraz liczbę wyznaczonych prostych x obliczamy następująco:

\(C_n^k={n\choose k}=\frac{n!}{k!(n-k)!}\)

Dla k=2 i n=10 mamy:

\(x=C_{10}^2={10\choose 2}=\frac{10!}{2!(10-2)!}=\frac{\cancel{8!}\cdot 9 \cdot 10}{2\cdot \cancel{8!}}=\frac{90}{2}=45\)

W przestrzeni punkty te wyznaczają tyle samo prostych

Odpowiedź

\(x = 45\)

Matura z matematyki

Zbiór zadań maturalnych z ubiegłych lat na poziomie podstawowym i rozszerzonym oraz centrum dowodzenia dla maturzystów.

Zbiór zadań z matematyki

Zbiór zadań z matematyki wraz z pełnymi rozwiązaniami. W naszej bazie zgromadziliśmy ponad tysiąc zadań.

WYKRESY ONLINE

Narysuj wykres funkcji w programie do szkicowania wykresów i odczytaj jego własności.

Zadania podobne

Zadanie nr 1.

Dane są dowolne proste \(a\) i \(b\). Określić figury \(a\cup b, \ a\cap b, \ a\setminus b, \ b\setminus a\).

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Dany jest okrąg \(k\) i prosta \(p\) przechodząca przez środek okręgu. Opisać figury: \(k\cup p, \ k\cap p, \ k\setminus p, \ p\setminus k\).

Pokaż rozwiązanie zadania.

Zadanie nr 3.

Dane są dwa trójkąty \(t_1\) i \(t_2\) usytuowane względem siebie tak, jak pokazuje rysunek.

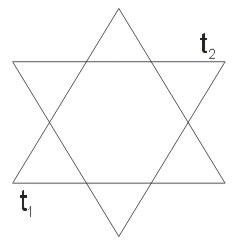
gwiazda

Zakreskować figury:

a) \(t_1\cup t_2\)

b) \(t_1\cap t_2\)

c) \(t_1\setminus t_2\)

d) \(t_1\setminus t_2\)

e) \((t_1\setminus t_2)\cup (t_2\setminus t_1)\)

Pokaż rozwiązanie zadania.

Zadanie nr 4.

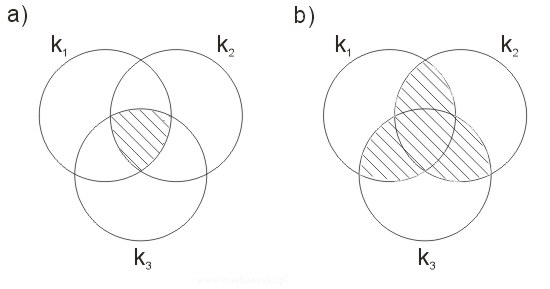
Opisać za pomocą działań na zbiorach część zakreskowaną kół \(k_1, k_2, k_3\):

figury

Pokaż rozwiązanie zadania.