Zadanie - układ równań II stopnia z dwiema niewiadomymi
Treść zadania:
Rozwiązać graficznie i rachunkowo układ równań
\(\begin{cases} xy-2=0 \\ y=-3x+3 \end{cases}\)
Rozwiązanie szczegółowe
Rozwiążemy najpierw układ równań graficznie. Sporządzimy wykres obu równań w jednym układzie współrzędnych.
\(xy-2=0\)
\(xy=2/:x (x\neq 0)\)
\(y=\frac{2}{x}\)
Wykresem tego równania jest hiperbola. Założyliśmy, że \(x\) jest różne od zera. Gdyby \(x\) było równe zeru, wówczas otrzymujemy równanie sprzeczne: \(0=2\). Sporządzamy tabelkę zmienności:
x-2-1-1/21/212y-1-2-4421Jeżeli chodzi o drugie równanie (\(y=-3x+3\)), to jego wykresem jest prosta. Poniżej tabelka zmienności funkcji (wystarczą dwa punkty):
x01y30Wykreślamy oba wykresy w jednym układzie współrzędnych.
Wykresy wydają się nie mieć punktów wspólnych, stąd wniosek, że układ równań nie ma rozwiązania.
Dlaczego punkty wspólne są rozwiązaniem układu? Otóż wszystkie punkty okręgu spełniają pierwsze równanie układu, punkty prostej spełniają drugie równanie, natomiast te punkty, które są wspólne dla obu wykresów, spełniają zarówno pierwsze, jak i drugie równanie. Dlatego stanowią rozwiązanie układu. W naszym przypadku nie ma takich punktów. Znajdźmy teraz rozwiązanie za pomocą rachunków.
Stosujemy metodę podstawienia:
\(\begin{cases}xy-2=0\\y=-3x+3\end{cases}\)
\(x(-3x+3)-2=0\)
\(-3x^2+3x-2=0\)
\(\Delta=b^2-4ac=3^2-4\cdot(-3)\cdot(-2)=9-24=-15<0\)
Ponieważ wyróżnik trójmianu kwadratowego jest ujemny, równanie nie posiada pierwiastków, a co za tym idzie, układ równań również nie posiada rozwiązań.
Odpowiedź
Układ równań nie ma rozwiązania.© medianauka.pl, 2010-02-05, ZAD-576


Zadania podobne
Zadanie nr 1.
Rozwiązać graficznie i rachunkowo układ równań
\(\begin{cases} (x-2)^2+(y-2)^2=1 \\ y=x+1 \end{cases}\)
Zadanie nr 2.
Rozwiązać graficznie i rachunkowo układ równań
\(\begin{cases} x^2+y^2=4 \\ xy=1 \end{cases}\)
Zadanie nr 3.
Rozwiązać graficznie i rachunkowo układ równań:
a) \(\begin{cases} (x+1)^2+(y+1)^2=4 \\ x=3 \\y=1 \end{cases}\)
b) \(\begin{cases} (x-1)^2+(y-1)^2=4 \\ x=3 \\y=1 \end{cases}\)
Zadanie nr 4.
Rozwiązać graficznie układ równań:
\(\begin{cases} (x-1)^2+(y-1)^2=2 \\ y=x^2 \end{cases}\)
Zadanie nr 5.
Dla jakich wartości parametru m układ równań:
\(\begin{cases} x^2+y^2=4 \\ y=3x+m \end{cases}\)
a) nie posiada rozwiązań
b) posiada jedno rozwiązanie
c) posiada dwa rozwiązania
d) posiada nieskończenie wiele rozwiązań?
Zadanie nr 6.
Rozwiązać graficznie i rachunkowo układ równań:
\(\begin{cases} y=\frac{1}{4}x^2-x+1 \\ (x-2)^2+(y-2)^2=4 \end{cases}\)
Zadanie nr 7.
Rozwiązać graficznie układy nierówności:
a) \(\begin{cases} (x-2)^2+(y-2)^2\leq 4 \\ (x-2)^2+(y-2)^2\geq 1 \end{cases}\)
b) \(\begin{cases} (x-1)^2+y^2\leq 4 \\ (x+1)^2+y^2\leq 4 \end{cases}\)
Zadanie nr 8.
Rozwiązać graficznie układ nierówności:
\(\begin{cases} x^2+y^2\leq 4 \\ y<x \\y>-x \end{cases}\)
Zadanie nr 9.
Zapisz za pomocą wzoru zbiór przedstawiony na rysunku (zakreskowane pole).
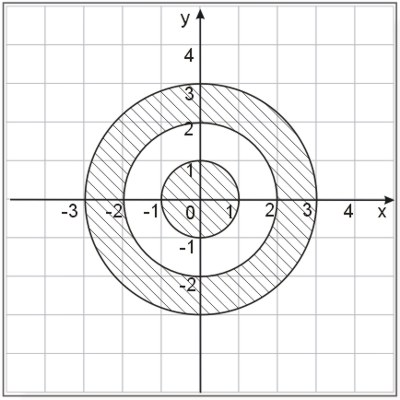

Zadanie nr 10 — maturalne.
W kartezjańskim układzie współrzędnych \((x,y)\) prosta \(l\) o równaniu \(x-y-2=0\) przecina parabolę o równaniu \(y=4x^2-7x+1\) w punktach \(A\) oraz \(B\). Odcinek \(AB\) jest średnicą okręgu \(O\). Punkt \(C\) leży na okręgu \(O\) nad prostą \(l\), a kąt \(BAC\) jest ostry i ma miarę \(\alpha\) taką, że \(tg\alpha=\frac{1}{3}\) (zobacz rysunek).
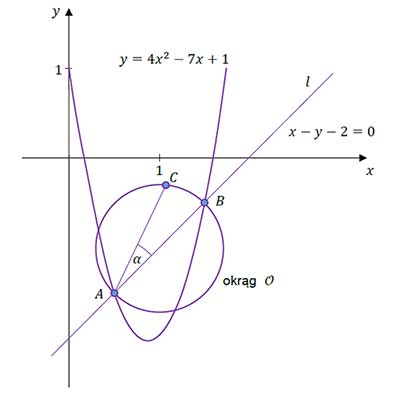
Oblicz współrzędne punktu \(C\). Zapisz obliczenia.






