Nierówność kwadratowa z dwiema niewiadomymi

Każdą z nierówności

\(ax^2+by^2+cxy+dx+ey+f<0\)

\(ax^2+by^2+cxy+dx+ey+f>0\)

\(ax^2+by^2+cxy+dx+ey+f\leq{0}\)

\(ax^2+by^2+cxy+dx+ey+f\geq{0}\)

gdzie \(a, b, c, d, e, f\) są dowolnymi liczbami i przynajmniej jedna z liczb \(a, b, c\) jest różna od zera, a \(x, y\) - są zmiennymi, nazywamy nierównością drugiego stopnia z dwiema niewiadomymi.

Przykłady

Przykłady nierówności pierwszego stopnia z dwiema niewiadomymi:

\(2xy+4y+6\geq{0}\)
\(x^2-y^2+xy+x+y+1>0\)
\({\frac{4x-y}{12}-\sqrt{7}x^2\leq{\sqrt{3}y^2-1}}\)

Definicja

Każdą parę liczb \((m,n)\), która spełnia nierówność drugiego stopnia z dwiema niewiadomymi (to znaczy, która podstawiona do nierówności \(m\) za \(x\) oraz \(n\) za \(y\) daje nierówność prawdziwą), nazywamy rozwiązaniem tej nierówności.

Przykład

Dana jest nierówność \(x^2-xy>0\). Jest nieskończenie wiele par liczb, które spełniają tę nierówność. Są to dla przykładu: (1,-1), (-1,1), (10,3) itd.

Interpretacja geometryczna

Interpretacją geometryczną w układzie współrzędnych nierówności drugiego stopnia z dwiema niewiadomymi jest figura geometryczna płaska wyznaczona przez wykres równania \(ax^2+by^2+cxy+dx+ey+f=0\).

Wykres dzieli płaszczyznę dwie części. Ta, która jest wykresem nierówności, zależy od znaku nierówności. Jeżeli nierówność jest ostra, do wykresu nierówności nie zalicza się samego wykresu, w przypadku nieostrej nierówności — wykres należy do wykresu nierówności razem z pozostałą częścią.

Przykład

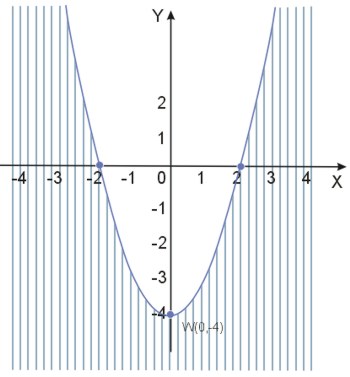
Rozwiązać nierówność \(4x^2-2y-8>0\).

Powyższą nierówność można rozwiązać graficznie. Przekształćmy ją.

\(4x^2-2y-8>0\)

\(-2y>-4x^2+8/:(-2)\)

\(y<2x^2-4\)

\(y<2(x^2-4)\)

\(y<2(x-2)(x+2)\)

Mamy więc do czynienia z parabolą. Są dwa miejsca zerowe: -2 i 2. Obliczmy jeszcze współrzędne wierzchołka paraboli:

\(\Delta=b^2-4ac=32\).

Zatem:

\(x_w=-\frac{b}{2a}=0\)

\(y_w=-\frac{\Delta}{4a}=-\frac{32}{8}=-4\)

Wykreślamy zatem w układzie współrzędnych parabolę o równaniu \(y=2x^2-4\) i zaznaczamy tę część płaszczyzny, która zawiera punkty o współrzędnych spełniających daną nierówność, zaznaczając, że krzywa też należy do wykresu tej nierówności.

wykres

Zadania z rozwiązaniami

Zadanie nr 1.

Rozwiązać graficznie nierówność:

a) \(x^2+y^2\leq 4\)

b) \(x^2+y^2>1\)

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Rozwiązać graficznie nierówność \(xy+2>1\).

Pokaż rozwiązanie zadania.

Zadanie nr 3.

Rozwiązać graficznie nierówność \(y\leq -x^2+x+2\).

Pokaż rozwiązanie zadania.

Inne zagadnienia z tej lekcji

Równanie okręgu

Równania i nierówności 2st. z 2 niewiadomymi