Zadania — równania i nierówności liniowe
Znajdziesz tutaj równania i nierówności liniowe o raz układy równań i nierówności liniowych. Wszystkie zadania są z rozwiązaniami. Są tu zadania autorskie oraz maturalne na poziomie podstawowym i rozszerzonym z kilku ostatnich lat.
Zadanie nr 2.
Dla jakiej wartości parametru \(a\) układ równań
\(\begin{cases} (a+1)x-3y+a=0 \\ ax+y+a+1=0 \end{cases}\)
nie ma rozwiązania?
Zadanie nr 3.
Dla jakiej wartości parametrów \(a, b, c\) układ równań
\(\begin{cases} (a+1)x-y=b \\ 2ax+y=c \end{cases}\)
ma nieskończenie wiele rozwiązań?
Zadanie nr 4.
Dla jakiej wartości parametru \(a\) układ równań
\(\begin{cases} (a-2)x+y=-3a+1 \\ -4x+(a+4)y=a-1 \end{cases}\)
ma jedno rozwiązanie?
Zadanie nr 5.
Rozwiązać układ równań
\(\begin{cases} \sqrt{2}x-(\sqrt{2}-1)y=3-2\sqrt{2} \\ (2+\sqrt{2})x+\sqrt{2}y=-2 \end{cases}\)
Zadanie nr 6.
Rozwiązać układ równań
\(\begin{cases} \frac{x-y}{2}=x+2 \\ y-x=\frac{x+1}{3} \end{cases}\)
Zadanie nr 7.
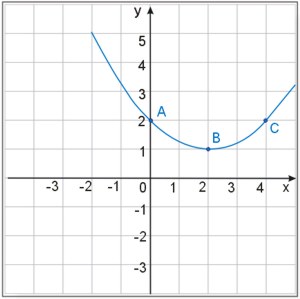
Znaleźć równanie paraboli, której fragment przedstawiono na rysunku:
Zadanie nr 8.
Znaleźć współrzędne punktu przecięcia się prostych o równaniach \(y=3x-5\) oraz \(y=-5x+3\)
Zadanie nr 9.
Rozwiązać układ równań metodą podstawiania:
a) \(\begin{cases} 3x-2y=-4 \\ x+3y=-5\end{cases}\)
b) \(\begin{cases} \sqrt{3}x+4y=1\\ x+2\sqrt{3}y=\sqrt{3}\end{cases}\)
Zadanie nr 10.
Rozwiązać układ równań metodą podstawiania:
a) \(\begin{cases} y-3x=2\\ -2y+6x=1 \end{cases}\)
b) \(\begin{cases} 2x+\frac{1}{2}y=\frac{1}{3}\\ -12x-3y=-2 \end{cases}\)
Zadanie nr 11.
Rozwiązać układ równań metodą przeciwnych współczynników:
a) \(\begin{cases} \frac{1}{2}x-2=y\\ \frac{1}{3}x+3=\frac{1}{4}y \end{cases}\)
b) \(\begin{cases} 5x+5y=-7\\ -3x-2y=4 \end{cases}\)
Zadanie nr 12.
Rozwiązać układ równań metodą przeciwnych współczynników:
a) \(\begin{cases} \sqrt{2}x-\sqrt{6}y=\sqrt{5}\\ 2x+4y=\sqrt{10} \end{cases}\)
b) \(\begin{cases} 2x+y=-\frac{1}{2}\\ -4x-2y=1 \end{cases}\)
c) \(\begin{cases} 3x-y=5\\-6x+2y=-1 \end{cases}\)
Zadanie nr 14.
Dane jest równanie: \(\sqrt{2}x+2y=1\). Dla jakich wartości parametru a para liczb \((1,a)\) spełnia to równanie?
Zadanie nr 15.
Dana jest nierówność \(5x-10y>1\). Dla jakich wartości parametru \(a\) para liczb \((-1,a)\) spełnia nierówność?
Zadanie nr 16.
Wyznaczyć zbiór rozwiązań nierówności:
a) \(-y-x\geq -1\)
b) \(2y-6x-4<0\)
c) \(y+x\geq 2y+x+1\)
Zadanie nr 17.
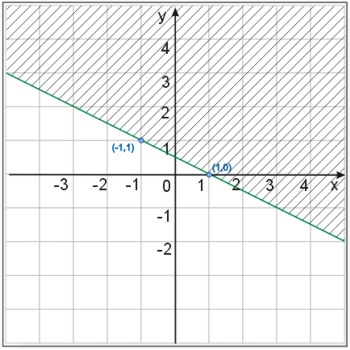
Opisać za pomocą nierówności półpłaszczyznę przedstawioną na rysunku:
Zadanie nr 18.
Rozwiązać nierówność:
a) \(\frac{1}{2}(x-1)+x\geq 5-2(x+2)\)
b) \((x-5)^2\geq (x+4)^2\)
c) \(\frac{2x-3}{5}>\frac{1-x}{2}\)
Zadanie nr 19.
Rozwiązać nierówność \(x^2+ax<(x-a)^2\) ze względu na niewiadomą \(x\).
Zadanie nr 20.
W pewnej liczbie dwucyfrowej liczba jedności jest o 4 większa od liczby dziesiątek. Znaleźć tę liczbę, jeśli wiadomo, że jest większa od 40 i mniejsza od 50.
Zadanie nr 21.
Dziadek jest dwa razy starszy od wnuczka. Kiedy suma ich wieku przekroczy 90 lat?
Zadanie nr 24.
Rozwiązać równanie:
a) \(5x-3=7x+8\)
b) \(\sqrt{2}x+1=x+\sqrt{2}\)
c) \(\frac{1}{2}x-\frac{3}{7}=\frac{x}{2}-2\)
Zadanie nr 27.
Dla jakiej wartości parametru \(m\) rozwiązaniem równania \(x-m+1=3x-2\) jest liczba 2?
Zadanie nr 28.
Rozwiązać równanie \(\frac{x}{m-2}+m=5\) ze względu na zmienną x.
Zadanie nr 29.
Jacek jest o 3 lata starszy od Maćka. Razem chłopcy mają 15 lat. Ile lat ma każdy z chłopców?
Zadanie nr 30.
Na jaki procent należy włożyć na lokatę 200 zł, aby po roku oszczędzania otrzymać 5 zł odsetek?
Zadanie nr 33.
Dany jest wektor \(\vec{AB}=[2,5]\) zaczepiony w punkcie \(A=(1,1)\). Znaleźć taki punkt \(C\), leżący na prostej \(y=2\), że pole trójkąta \(ABC\) jest równe 10.
Zadanie nr 34.
Rybak złowił szczupaka. Na pytanie, jak wielka jest ryba, odpowiedział zagadkowo: "Łeb szczupaka mierzy 6 cm, tułów ma długość taką jak głowa i ogon razem, przy czym trzy czwarte ogona mierzą tyle ile głowa i ćwierć długości głowy". Jaką długość ma szczupak?

Zadanie nr 36 - maturalne.
Proste o równaniach \(2x-3y=4\) i \(5x-6y=7\) przecinają się w punkcie \(P\). Stąd wynika, że:
A. \(P=(1,2)\)
B. \(P=(-1,2)\)
C. \(P=(-1,-2)\)
D. \(P=(1,-2)\)

Zadanie nr 37 - maturalne.
Wyznacz wszystkie wartości parametru \(a\), dla których wykresy funkcji \(f\) i \(g\), określonych wzorami \(f(x)=x-2\) oraz \(g(x)=5-ax\), przecinają się w punkcie o obu współrzędnych dodatnich.

Zadanie nr 38 - maturalne.
Układ równań
\(\begin{cases}x-y=3\\ 2x+0,5y=4 \end{cases}\)
opisuje w układzie współrzędnych na płaszczyźnie:
A. zbiór pusty.
B. dokładnie jeden punkt.
C. dokładnie dwa różne punkty.
D. zbiór nieskończony.

Zadanie nr 39 - maturalne.
Ile liczb całkowitych x spełnia nierówność \(\frac{2}{7}<\frac{x}{14}<\frac{4}{3}\) ?
A. 14
B. 15
C. 16
D. 17

Zadanie nr 40 - maturalne.
W układzie współrzędnych są dane punkty \(A=(-43,-12)\), \(B=(50,19)\). Prosta AB przecina oś \(Ox\) w punkcie \(P\). Oblicz pierwszą współrzędną punktu \(P\).

Zadanie nr 41 - maturalne.
Dana jest funkcja \(f\) określona wzorem
\(f(x)=\begin{cases}x-2 \quad dla \quad x\leq0\\||x+3|-4| \quad dla \quad x>0 \end{cases}\).
Równanie \(f(x)=1\) ma dokładnie
A. jedno rozwiązanie.
B. dwa rozwiązania.
C. cztery rozwiązania.
D. pięć rozwiązań.

Zadanie nr 42 - maturalne.
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
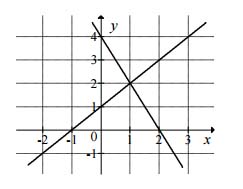
Wskaż ten układ:
A. \(\begin{cases}y=x+1\\y=-2x+4\end{cases}\)
B. \(\begin{cases}y=x-1\\y=2x+4\end{cases}"\)
C. \(\begin{cases}y=x-1\\y=-2x+4\end{cases}"\)
D. \(\begin{cases}y=x+1\\y=2x+4\end{cases}\)

Zadanie nr 43 - maturalne.
Wskaż rysunek, na którym jest przedstawiony zbiór wszystkich rozwiązań nierówności \(2-3x≥4\)
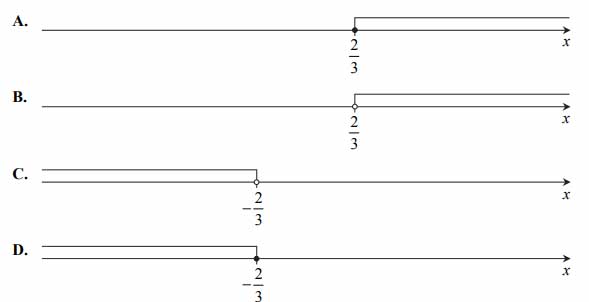

Zadanie nr 45 - maturalne.
Zbiorem wszystkich rozwiązań nierówności \(\frac{(1-2x)}{2}>\frac{1}{3}\) jest przedział:
- \((-\infty;\frac{1}{6})\)
- \((-\infty;\frac{2}{3})\)
- \((\frac{1}{6};+\infty)\)
- \((\frac{2}{3};+\infty)\)

Zadanie nr 47 - maturalne.
Para liczb \(x=2\) i \(y=2\) jest rozwiązaniem układu równań
\(\begin{cases} ax+y=5\\-2x+3y=2a\end{cases}\)
dla:
A. \(a=-1\)
B. \(a=1\)
C. \(a=-2\)
D. \(a=2\)

Zadanie nr 48 - maturalne.
Wyznacz wszystkie wartości parametru \(a\), dla których równanie \(|x−5|=(a−1)^2−4\) ma dwa różne rozwiązania dodatnie.

Zadanie nr 49 - maturalne.
Zbiorem wszystkich rozwiązań nierówności \(\frac{(2-x)}{2}-2x\geq 1\) jest przedział
A. \(\langle 0, +\infty)\)
B. \((−\infty, 0\rangle\)
C. \((−\infty, 5\rangle\)
D. \((−\infty,\frac{1}{3}\rangle\)

Zadanie nr 50 - maturalne.
Na rysunku obok przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań. Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku.
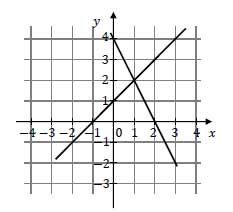
A. \(\begin{cases}y=x+1\\y=-2x+4\end{cases}\)
B. \(\begin{cases}y=x-1\\y=2x+4\end{cases}\)
C. \(\begin{cases}y=x-1\\y=2x+4\end{cases}\)
D. \(\begin{cases}y=x+1\\y=2x+4\end{cases}\)

Zadanie nr 51 - maturalne.
Liczba różnych pierwiastków równania \(3x+|x-4|=0\) jest równa
A. 0
B. 1
C. 2
D. 3

Zadanie nr 52 - maturalne.
Prosta przechodząca przez punkty \(A=(8, −6)\) i \(B=(5, 15)\) jest styczna do okręgu o środku w punkcie \(O=(0, 0)\). Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą AB.

Zadanie nr 53 - maturalne.
Rozwiązaniem układu równań \(\begin{cases} 11x-11y=1\\22x+22y=-1\end{cases}\) jest para liczb \(x=x_0, y=y_0\). Wtedy
A. \(x_0>0\) i \(y_0>0\)
B. \(x_0>0\) i \(y_0<0\)
C. \(x_0<0\) i \(y_0>0\)
D. \(x_0<0\) i \(y_0<0\)

Zadanie nr 55 - maturalne.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zbiorem wszystkich rozwiązań nierówności \(-2(x+3)\leq \frac{2-x}{3}\) jest przedział
A. \((-\infty,-4]\)
B. \((-\infty,4]\)
C. \([-4,\infty)\)
D. \([4,\infty)\)

Zadanie nr 56 - maturalne.
Rozwiąż nierówność:
\(\sqrt{x^2+4x+4}<\frac{25}{3}-\sqrt{x^2-6x+9}\)
Zapisz obliczenia. Wskazówka: skorzystaj z tego, że \(\sqrt{a^2}=|a|\) dla każdej liczby rzeczywistej \(a\).
Liczba odnalezionych zadań w zbiorze: 56.
Oznaczenia
 Zadania maturalne — poziom podstawowy.
Zadania maturalne — poziom podstawowy.
 Zadania maturalne — poziom rozszerzony.
Zadania maturalne — poziom rozszerzony.