Zadania — równania i nierówności kwadratowe
Znajdziesz tutaj równania i nierówności kwadratowe o raz układy równań i nierówności kwadratowych. Wszystkie zadania są z rozwiązaniami. Są tu zadania autorskie oraz maturalne na poziomie podstawowym i rozszerzonym z kilku ostatnich lat.
Zadanie nr 1.
Dla jakiej wartości parametru \(x\) prawdziwa jest równość \(\sqrt{(x^2-2x+1)^2}=x^2-2x+1\)?
Zadanie nr 3.
Dla jakiej wartości parametru \(m\) równanie \(mx^2+4mx-m+1=0\) ma jedno rozwiązanie? Znajdź to rozwiązanie?
Zadanie nr 7.
Dla jakich wartości parametru \(m\) suma odwrotności pierwiastków równania \(x^2-2(m+1)x+(m^2+3m-18)=0\) ma wartość ujemną?
Zadanie nr 9.
Napisać równanie okręgu, który został zilustrowany na poniższym rysunku.
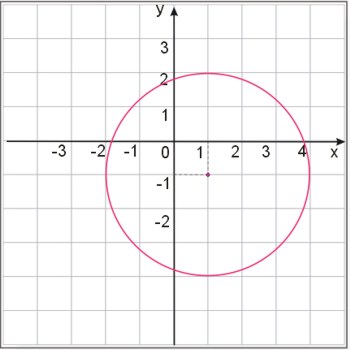
Zadanie nr 12.
Rozwiązać graficznie nierówność:
a) \(x^2+y^2\leq 4\)
b) \(x^2+y^2>1\)
Zadanie nr 15.
Rozwiązać graficznie i rachunkowo układ równań
\(\begin{cases} (x-2)^2+(y-2)^2=1 \\ y=x+1 \end{cases}\)
Zadanie nr 16.
Rozwiązać graficznie i rachunkowo układ równań
\(\begin{cases} xy-2=0 \\ y=-3x+3 \end{cases}\)
Zadanie nr 17.
Rozwiązać graficznie i rachunkowo układ równań
\(\begin{cases} x^2+y^2=4 \\ xy=1 \end{cases}\)
Zadanie nr 18.
Rozwiązać graficznie i rachunkowo układ równań:
a) \(\begin{cases} (x+1)^2+(y+1)^2=4 \\ x=3 \\y=1 \end{cases}\)
b) \(\begin{cases} (x-1)^2+(y-1)^2=4 \\ x=3 \\y=1 \end{cases}\)
Zadanie nr 19.
Rozwiązać graficznie układ równań:
\(\begin{cases} (x-1)^2+(y-1)^2=2 \\ y=x^2 \end{cases}\)
Zadanie nr 20.
Dla jakich wartości parametru m układ równań:
\(\begin{cases} x^2+y^2=4 \\ y=3x+m \end{cases}\)
a) nie posiada rozwiązań
b) posiada jedno rozwiązanie
c) posiada dwa rozwiązania
d) posiada nieskończenie wiele rozwiązań?
Zadanie nr 21.
Rozwiązać graficznie i rachunkowo układ równań:
\(\begin{cases} y=\frac{1}{4}x^2-x+1 \\ (x-2)^2+(y-2)^2=4 \end{cases}\)
Zadanie nr 22.
Rozwiązać graficznie układy nierówności:
a) \(\begin{cases} (x-2)^2+(y-2)^2\leq 4 \\ (x-2)^2+(y-2)^2\geq 1 \end{cases}\)
b) \(\begin{cases} (x-1)^2+y^2\leq 4 \\ (x+1)^2+y^2\leq 4 \end{cases}\)
Zadanie nr 23.
Rozwiązać graficznie układ nierówności:
\(\begin{cases} x^2+y^2\leq 4 \\ y<x \\y>-x \end{cases}\)
Zadanie nr 24.
Zapisz za pomocą wzoru zbiór przedstawiony na rysunku (zakreskowane pole).
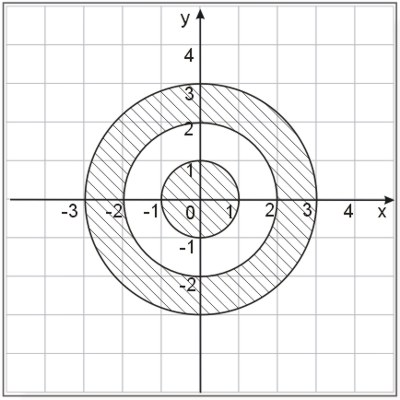
Zadanie nr 25.
Rozwiązać nierówność:
a) \(x^2+2x-3\geq 0\)
b) \(-x^2+\frac{3}{4}x-\frac{1}{8}> 0\)
c) \(-x^2+2\leq 0\)
Zadanie nr 26.
Rozwiązać nierówność:
a) \(\sqrt{3}x^2+\sqrt{2}x+1< 0\)
b) \(-x^2-2x-5\geq 0\)
Zadanie nr 27.
Rozwiązać nierówność:
a) \(x^2+8x+16> 0\)
b) \(-x^2+2\sqrt{2}x-2\geq 0\)
Zadanie nr 28.
Dla jakich wartości parametru \(m\) nierówność \(x^2-2x-m+1\leq 0\) ma jedno rozwiązanie \(x=1\)?
Zadanie nr 29.
Dla jakich wartości parametru \(m\) zbiorem rozwiązań nierówności \(x^2+mx-1+m> 0\) jest:
a) zbiór liczb rzeczywistych?
b) zbiór pusty?
Zadanie nr 30.
Rozwiązać równanie kwadratowe:
a) \(x^2+4x-5=0\)
b) \(x^2-22x+121=0\)
c) \(x^2+2x+7=0\)
Zadanie nr 31.
Rozwiązać równanie:
a) \(x^2-\frac{1}{4}x-\frac{1}{8}=0\)
b) \(x^2-10x-119=0\)
Zadanie nr 32.
Znaleźć wszystkie równania kwadratowe, których rozwiązaniem są liczby \(\sqrt{2}, \ \frac{1}{2}\).
Zadanie nr 36.
Kwadrat różnicy pierwiastków równania kwadratowego \(x^2-x+m=0\) jest równy 17. Znaleźć rozwiązanie tego równania.
Zadanie nr 37.
Suma kwadratów pierwiastków równania kwadratowego \(x^2+dx+1=0\) jest równa 7. Znaleźć rozwiązanie tego równania.
Zadanie nr 38.
Znaleźć równanie kwadratowe, którego suma kwadratów pierwiastków jest równa \(\frac{17}{4}\), a suma odwrotności pierwiastków jest równa \(\frac{3}{2}\).
Zadanie nr 39.
Rozwiązać równanie kwadratowe \(x^2+mx-3=0\), jeśli wiadomo, że suma odwrotności pierwiastków równania jest równa 2.
Zadanie nr 42.
Rozwiązać równanie \(\frac{3}{x-a}=\frac{x+a}{1-x}\) w zależności od parametru \(a\).
Zadanie nr 43.
Rozwiązać równanie \(\frac{2}{x-a}=\frac{x-a}{x}\) w zależności od parametru \(a\).
Zadanie nr 44.
Określić liczbę rozwiązań równania \((a+3)x^2-(a+1)x+1=0\) w zależności od parametru \(a\).
Zadanie nr 45.
Dla jakiej wartości parametru \(m\) równanie \(m^2x^2-6x+9=0\) ma jedno rozwiązanie?
Zadanie nr 46.
Znaleźć taką wartość parametru m, dla której suma kwadratów pierwiastków równania \(x^2-mx-m-1=0\) jest najmniejsza.
Zadanie nr 48.
Znaleźć równanie okręgu opisanego na trójkącie równobocznym, wyznaczonym przez punkty \(A=(1,1), B=(5,1), C=(3,2\sqrt{3}+1)\).
Zadanie nr 49.
Dany jest punkt \(A=(-1,1)\). Znaleźć punkt \(B\), jeżeli wiadomo, że \(|\vec{AB}|=4\).

Zadanie nr 51 - maturalne.
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych \(x\) i \(y\) takich, że \(x^2+y^2=2\), prawdziwa jest nierówność \(x+y\leq 2\).

Zadanie nr 52 - maturalne.
Dany jest trójmian kwadratowy \(f(x)=x^2+2(m+1)x+6m+1\). Wyznacz wszystkie rzeczywiste wartości parametru m, dla których ten trójmian ma dwa różne pierwiastki \(x_1\), \(x_2\) tego samego znaku, spełniające warunek \(|x_1-x_2|<3\).

Zadanie nr 54 - maturalne.
Dany jest trójmian kwadratowy \(f(x)=(m+1)x^2+2(m-2)x-m+4\). Wyznacz wszystkie wartości parametru \(m\), dla których trójmian \(f\) ma dwa różne pierwiastki rzeczywiste \(x_1, x_2\), spełniające warunek \(x_1^2-x_2^2=x_1^4-x_2^4\).

Zadanie nr 55 - maturalne.
Liczba punktów wspólnych okręgu o równaniu \((x+2)^2+(y-3)^2=4\) z osiami układu współrzędnych jest równa:
A. 0
B. 1
C. 2
D. 4

Zadanie nr 56 - maturalne.
Turysta zwiedzał zamek stojący na wzgórzu. Droga łącząca parking z zamkiem ma długość 2,1 km. Łączny czas wędrówki turysty z parkingu do zamku i z powrotem, nie licząc czasu poświęconego na zwiedzanie, był równy 1 godzinę i 4 minuty. Oblicz, z jaką średnią prędkością turysta wchodził na wzgórze, jeżeli prędkość ta była o 1 km/h mniejsza od średniej prędkości, z jaką schodził ze wzgórza.

Zadanie nr 57 - maturalne.
Równość \((x\sqrt{2} - 2)^2 = (\sqrt{2} + 2)^2\) jest
A. prawdziwa dla \(x=\sqrt{2}\)
B. prawdziwa dla \(x=-\sqrt{2}\)
C. prawdziwa dla \(x=-1\)
D. fałszywa dla każdej liczby \(x\)

Zadanie nr 58 - maturalne.
Dany jest okrąg o środku \(S=(2,3)\) i promieniu \(r=5\). Który z podanych punktów leży na tym okręgu?
A. \(A=(-1, 7)\)
B. \(B=(2, 3)\)
C. \(C=(3, 2)\)
D. \(D=(5, 3)\)

Zadanie nr 59 - maturalne.
Wyznacz wszystkie wartości parametru \(m\), dla których równanie \(4x^2−6mx+(2m+ 3)(m− 3)=0\) ma dwa różne rozwiązania rzeczywiste \(x_1\) i \(x_2\), przy czym \(x_1<x_2\), spełniające warunek \((4x_1-4x_2-1)(4x_1-4x_2+1)<0\).

Zadanie nr 60 - maturalne.
Wyznacz równanie okręgu przechodzącego przez punkty \(A=(−5, 3)\) i \(B=(0, 6)\), którego środek leży na prostej o równaniu \(x−3y+1=0\).

Zadanie nr 61 - maturalne.
Średnicą okręgu jest odcinek \(KL\), gdzie \(K=(6,8)\), \(L=(−6, − 8)\). Równanie tego okręgu ma postać
A. \(x^2+y^2=200\)
B. \(x^2+y^2=100\)
C. \(x^2+y^2=400\)
D. \(x^2+y^2=300\)

Zadanie nr 63 - maturalne.
Wyznacz wszystkie wartości parametru \(m\), dla których równanie \(x^2 + (m+1)x−m^2+1=0\) ma dwa rozwiązania rzeczywiste \(x_1\) i \(x_2\) \((x_1\neq x_2)\), spełniające warunek \(x^3_1+x^3_2>−7x_1x_2\).

Zadanie nr 65 - maturalne.
Dane są okręgi o równaniach \(x^2+y^2−12x−8y+43=0\) i \(x^2+y^2−2ax+4y+a^2−77=0\). Wyznacz wszystkie wartości parametru \(a\), dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.

Zadanie nr 66 - maturalne.
Wyznacz wszystkie wartości parametru \(m\), dla których funkcja kwadratowa \(f\) określona wzorem \(f(x)=(2m +1)x^2+(m+2)x+m−3\) ma dwa różne pierwiastki rzeczywiste \(x_1, x_2\), spełniające warunek \((x_1- x_2)^2+5x_1x_2 \geq 1\).

Zadanie nr 68 - maturalne.
Dane jest równanie kwadratowe \(x^2−(3m+2)x+2m^2+7m−15=0\) z niewiadomą \(x\). Wyznacz wszystkie wartości parametru \(m\), dla których różne rozwiązania \(x_1\) i \(x_2\)tego równania istnieją i spełniają warunek \(2x^2_1+5x_1x_2+2x^2_2=2\).

Zadanie nr 69 - maturalne.
W każdym n-kącie wypukłym (n≥ 3) liczba przekątnych jest równa n(n-3)/2. Wielokątem wypukłym, w którym liczba przekątnych jest o 25 większa od liczby boków, jest
A. siedmiokąt.
B. dziesięciokąt.
C. dwunastokąt.
D. piętnastokąt.

Zadanie nr 71 - maturalne.
Wyznacz wszystkie wartości parametru \(m\), dla których trójmian kwadratowy \(4x^2-2(m+1)x+m\) ma dwa różne pierwiastki rzeczywiste \(x_1\) oraz \(x_2\), spełniające warunki: \(x_1 \neq 0, x_2\neq 0\) oraz \(x_1+x_2\leq \frac{1}{x_1}+\frac{1}{x_2}\).

Zadanie nr 73 - maturalne.
Wyznacz wszystkie wartości parametru \(m\), dla których równanie \(x^2-(m+1)x+m=0\) ma dwa różne rozwiązania rzeczywiste \(x_1\) oraz \(x_2\), spełniające warunki: \(x_1\neq 0, x_2\neq 0\) oraz \(\frac{1}{x_1}+\frac{1}{x_2}+2=\frac{1}{x_1^2} +\frac{1}{x_2^2}\).

Zadanie nr 74 - maturalne.
Wyznacz wszystkie wartości parametru \(m\neq 2\), dla których równanie
\(x^2+4x-\frac{m-3}{m-2}=0\)
ma dwa różne rozwiązania rzeczywiste \(x_1, x_2\) spełniające warunek \(x_1^3+x_2^3>-28\). Zapisz obliczenia.

Zadanie nr 75 - maturalne.
W kartezjańskim układzie współrzędnych \((x,y)\) prosta \(l\) o równaniu \(x-y-2=0\) przecina parabolę o równaniu \(y=4x^2-7x+1\) w punktach \(A\) oraz \(B\). Odcinek \(AB\) jest średnicą okręgu \(O\). Punkt \(C\) leży na okręgu \(O\) nad prostą \(l\), a kąt \(BAC\) jest ostry i ma miarę \(\alpha\) taką, że \(tg\alpha=\frac{1}{3}\) (zobacz rysunek).
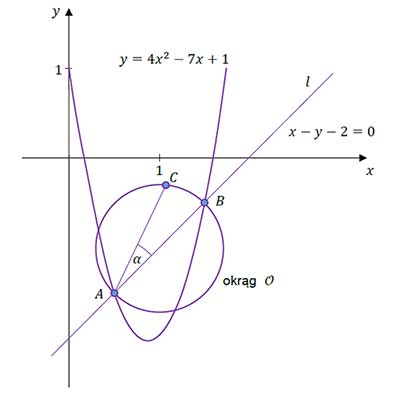
Oblicz współrzędne punktu \(C\). Zapisz obliczenia.
Liczba odnalezionych zadań w zbiorze: 75.
Oznaczenia
 Zadania maturalne — poziom podstawowy.
Zadania maturalne — poziom podstawowy.
 Zadania maturalne — poziom rozszerzony.
Zadania maturalne — poziom rozszerzony.