Nauka » Matematyka » Równanie kwadratowe z parametrem

Zadanie - równanie kwadratowe z parametrem

Określić liczbę rozwiązań równania

w zależności od parametru a.

Rozwiązanie zadania ze szczegółowymi wyjaśnieniami

Aby nasze równanie było równaniem kwadratowym, współczynnik przy x² musi być różny od zera.

Mamy postać równania kwadratowego. Obliczamy wyróżnik trójmianu kwadratowego:

$(a+3)x^2-(a+1)x+1=0 \\ a_1=a+3\\ b_1=-(a+1) \\c_1=1 \\ \Delta=b_1^2-4a_1c_1=[-(a+1)]^2-4(a+3)\cdot 1=\\ =(a+1)^2-4(a+3)=a^2+2a+1-4a-12=\\ =a^2-2a-11$

W zależności od znaku wyróżnika równanie może mieć jedno, dwa lub zero rozwiązań.

1) Jeżeli ∆>0 równanie kwadratowe ma dwa rozwiązania.

$\Delta>0\\ a^2-2a-11>0$

Rozwiązujemy nierówność kwadratową:

$\Delta_a=(-2)^2+4\cdot 11\cdot 1=48 \\ \sqrt{\Delta}=\sqrt{48}=\sqrt{16\cdot 3}=4\sqrt{3}\\ a_1=\frac{2-4\sqrt{3}}{2}=1-2\sqrt{3}\appr -2,5 \\ a_2=\frac{2+4\sqrt{3}}{2}=1+2\sqrt{3}\appr 4,5$

Ramiona paraboli a²-2a-11 są skierowane do góry, funkcja ma dwa miejsca zerowe, interesują nas wartości dodatnie. Pamiętając o dziedzinie równania (jeżeli a jest równe -3, równanie staje się równaniem liniowym i nie może mieć dwóch rozwiązań), odczytujemy rozwiązanie z wykresu (zakreskowany niebieski obszar):

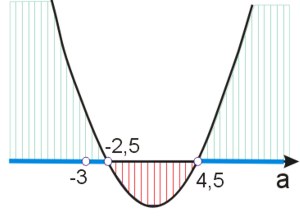
$a\in(-\infty;-3)\cup (-3; 1-2\sqrt{3})\cup (1+2\sqrt{3};+\infty)$

2) Jeżeli ∆=0 równanie kwadratowe ma jedno rozwiązanie. Odczytujemy je z powyższego rysunku (punkty na osi liczbowej)

$\Delta=0\\ a_1=1-2\sqrt{3} \\ a_2=1+2\sqrt{3} \\ a_3=-3$

Ten ostatni pierwiastek wynika z tego, że gdy a=-3 mamy równanie liniowe, które ma jedno rozwiązanie

3) Jeżeli ∆<0 równanie kwadratowe nie ma rozwiązania.

Rozwiązanie odczytujemy z powyższego wykresu (zakreskowany czerwony obszar).

$a\in (1-2\sqrt{3};1+2\sqrt{3})$

Odpowiedź

Równanie

ma dwa rozwiązania dla $a\in(-\infty;-3)\cup (-3; 1-2\sqrt{3})\cup (1+2\sqrt{3};+\infty)$ , jedno rozwiązanie dla $a=-3, \ a=1-2\sqrt{3}, \ a=1+2sqrt{3}$ i zero rozwiązań dla $a\in (1-2\sqrt{3};1+2\sqrt{3})$

Zadania podobne

Zadanie - równanie kwadratowe z parametrem
Dla jakiej wartości parametru m równanie

ma jedno rozwiązanie? Znajdź to rozwiązanie.

Pokaż rozwiązanie zadania

Zadanie - równanie algebraiczne i kwadratowe z parametrem
Dla jakich wartości parametru m suma odwrotności pierwiastków równania x^2-2(m+1)x+(m^2+3m-18)=0

ma wartość ujemną?

Pokaż rozwiązanie zadania

Zadanie - równanie kwadratowe z parametrem
Rozwiązać równanie $\frac{3}{x-a}=\frac{x+a}{1-x}$ w zależności od parametru a.

Pokaż rozwiązanie zadania

Zadanie - równanie kwadratowe z parametrem
Rozwiązać równanie $\frac{2}{x-a}=\frac{x-a}{x}$ w zależności od parametru a.

Pokaż rozwiązanie zadania

Zadanie - równanie kwadratowe z parametrem
Dla jakiej wartości parametru m równanie

ma jedno rozwiązanie?

Pokaż rozwiązanie zadania

Zadanie - równanie z parametrem
Znaleźć taką wartość parametru m, dla której suma kwadratów pierwiastków równania

jest najmniejsza.

Pokaż rozwiązanie zadania

Zadanie maturalne nr 12, matura 2016 (poziom rozszerzony)
Dany jest trójmian kwadratowy

. Wyznacz wszystkie rzeczywiste wartości parametru m, dla których ten trójmian ma dwa różne pierwiastki x₁, x₂ tego samego znaku, spełniające warunek |x₁-x₂|<3.

Pokaż rozwiązanie zadania

Zadanie maturalne nr 13, matura 2015 (poziom rozszerzony)
Dany jest trójmian kwadratowy

. Wyznacz wszystkie wartości parametru m, dla których trójmian f ma dwa różne pierwiastki rzeczywiste x₁, x₂, spełniające warunek

.

Pokaż rozwiązanie zadania

Niektóre treści nie są dostosowane do Twojego profilu. Jeżeli jesteś pełnoletni możesz wyrazić zgodę na przetwarzanie swoich danych osobowych. W ten sposób będziesz miał także wpływ na rozwój naszego serwisu.