Nierówność z dwiema niewiadomymi
Każdą z nierówności
\(ax+by+c<0\)
\(ax+by+c>0\)
\(ax+by+c\leq{0}\)
\(ax+by+c\geq{0}\)
gdzie \(a, b, c\) są dowolnymi liczbami i przynajmniej jedna z liczb \(a\) lub \(b\) jest różna od zera, a \(x, y\) są zmiennymi, nazywamy nierównością pierwszego stopnia z dwiema niewiadomymi.
Przykłady
Przykłady nierówności pierwszego stopnia z dwiema niewiadomymi:
- \(2x+4y+6\geq{0}\)
- \(x-y>0\)
- \(\frac{4x-y}{12}-\sqrt{2}\leq{\sqrt{3}-1}\)
Definicja
Każdą parę liczb \((m,n)\), która spełnia nierówność pierwszego stopnia z dwiema niewiadomymi (to znaczy, która podstawiona do nierówności \(m\) za \(x\) oraz \(n\) za \(y\) daje nierówność prawdziwą) nazywamy rozwiązaniem tej nierówności.
Przykłady
Dana jest nierówność: \(2x+y-1>0\). Jest nieskończenie wiele par liczb, które spełniają tę nierówność. Są to dla przykładu \((3,8), (3,-1), (-1,4)\) itd.
Interpretacja geometryczna
Interpretacją geometryczną w układzie współrzędnych nierówności pierwszego stopnia z dwiema niewiadomymi jest półpłaszczyzna wyznaczona przez prostą o równaniu \(ax+by+c=0\).
Prosta wyznacza na płaszczyźnie dwie półpłaszczyzny. To, która jest wykresem nierówności, zależy od znaku nierówności. Jeżeli nierówność jest ostra, do wykresu nierówności nie zalicza się samej prostej wyznaczającej półpłaszczyznę, w przypadku nieostrej nierówności — prosta należy do wykresu nierówności razem z półpłaszczyzną.
Przykłady
Rozwiązać nierówność \(2x+y-1\geq{0}\).
Powyższą nierówność można rozwiązać graficznie. Przekształćmy ją.
\(2x+y-1\geq{0}\)
\(y\geq -2x+1\)
Wykreślamy zatem w układzie współrzędnych prostą o równaniu \(y=-2x+1\) i zaznaczamy tę część płaszczyzny, która zawiera punkty o współrzędnych spełniających daną nierówność, zaznaczając, że prosta też należy do wykresu tej nierówności.
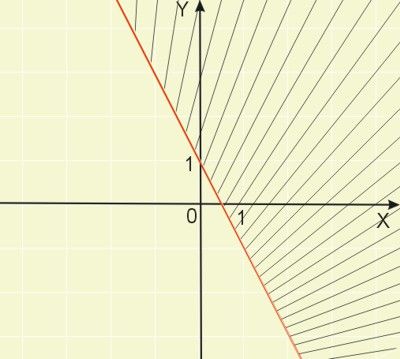
Zadania z rozwiązaniami

Zadanie nr 1.
Dana jest nierówność \(5x-10y>1\). Dla jakich wartości parametru \(a\) para liczb \((-1,a)\) spełnia nierówność?

Zadanie nr 2.
Wyznaczyć zbiór rozwiązań nierówności:
a) \(-y-x\geq -1\)
b) \(2y-6x-4<0\)
c) \(y+x\geq 2y+x+1\)

Zadanie nr 3.
Opisać za pomocą nierówności półpłaszczyznę przedstawioną na rysunku:
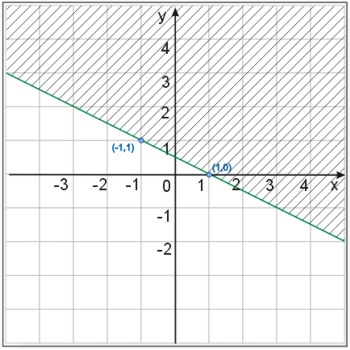
Powiązane materiały
© medianauka.pl, 2009-07-02, A-257
Data aktualizacji artykułu: 2023-05-06

 Równanie z dwiema niewiadomymi
Równanie z dwiema niewiadomymi Równianie i nierówność z 2 niewiadomymi
Równianie i nierówność z 2 niewiadomymi



