Wzór dwumianowy Newtona

Wzór dwumianowy Newtona jest to wzór w postaci:

\((a+b)^n={n \choose 0}a^n+{n \choose 1}a^{n-1}b+{n \choose 2}a^{n-2}b^2+...+{n \choose n}b^n\)

Za pomocą tego wzoru możemy wyrazić każdą naturalną potęgę sumy.

Zapis \(n \choose k\) oznacza symbol Newtona.

Przykłady

\((a+b)^4={4\choose 0}a^4+{4 \choose 1}a^3b+{4 \choose 2}a^2b^2+{4 \choose 3}ab^3+{4 \choose 4}b^4=\)

\(a^4+\frac{4!}{1!3!}a^3b+\frac{4!}{2!2!}a^2b^2+\frac{4!}{3!1!}ab^3+b^4= \)

\( =a^4+4a^3b+6a^2b^2+4ab^3+b^4\)

Dwumian Newtona nie jest łatwym do zapamiętania wzorem. Jednak ułatwia to tak zwany trójkąt Pascala.

Trójkąt Pascala

Współczynniki dwumianowe \(n \choose k\) można znajdować na podstawie tak zwanego trójkąta Pascala.

Jest to tablica liczb w kształcie trójkąta, w której reguła tworzenia kolejnych wierszy jest następująca:

każdy wiersz zaczyna się i kończy jedynką,
każdy z pozostałych wyrazów jest sumą 2 kolejnych wyrazów wiersza poprzedniego — umieszcza się go poniżej przerwy między tymi wyrazami.

Poniżej przedstawiony został trójkąt Pascala do wielkości \(n=15\).

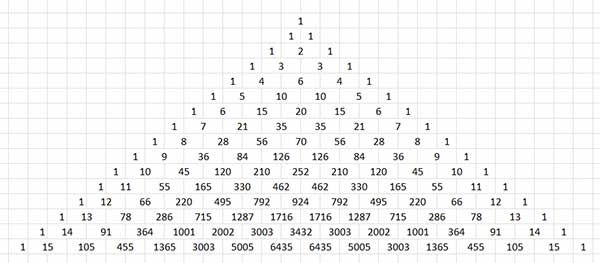
Z powyższego rysunku możemy wprost odczytać odpowiednie współczynniki dwumianowe.

Weźmy dla przykładu piąty rząd dla \(n=5\). Otrzymujemy od razu wzór na piątą potęgę sumy dwóch liczb: \((a+b)^5=a^5+5a^4b+10a^2b^2+10a^2b^3+5ab^4+b^5\).

Szczególnym, przypadkiem dwumianu Newtona są wzory skróconego mnożenia.

Zadania z rozwiązaniami

Zadanie nr 1 — maturalne.

Po przekształceniu wyrażenia algebraicznego \((x\sqrt{2}+y\sqrt{3})^4\) do postaci \(ax^4+bx^3y+cx^2y^2+dxy^3+ey^4\) współczynnik \(c\) jest równy

A. \(6\)

B. \(36\)

C. \(8\sqrt{6}\)

D. \(12\sqrt{6}\)

Pokaż rozwiązanie zadania.

Powiązane materiały

Działania na potęgach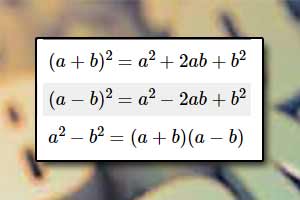

Wzory skróconego mnożenia

Potęgowanie