Działania na potęgach
Dla każdej pary liczb rzeczywistych \(a\) i \(b\) oraz liczb naturalnych \(m\) i \(n\) dodatnich prawdziwe są wzory:
- \(a^m\cdot a^n=a^{m+n}\)
- \(a^m:a^n=a^{m-n}, a\neq 0, m>n\)
- \((a^m)^n=a^{m\cdot n}\)
- \(a^n\cdot b^n = (ab)^n\)
- \(a^n:b^n=(a:b)^n, b\neq 0\)
Uwaga! Powyższe wzory są prawdziwe także dla potęg o wykładnikach całkowitych i rzeczywistych (warunek \(m>n\) dla wzoru drugiego nie jest już konieczny).
Przykłady
Iloczyn (mnożenie) potęg
A oto przykłady na zastosowanie pierwszego wzoru:
- \(5^2\cdot 5^{17}=5^{2+17}=5^{19}\)
- \((\frac{1}{8})^7\cdot (\frac{1}{8})^7=(\frac{1}{8})^{7+7}=(\frac{1}{8})^{14}\)
- \((-9)^4\cdot (-9)^9=(-9)^{4+9}=(-9)^{13}\)
- \(5^{-20}\cdot 5^{20}=5^{-20+20}=5^0=1\)
Dzielenie potęg
A oto przykłady na zastosowanie drugiego wzoru:
- \(5^{17}:5^{2}=5^{17-2}=5^{15}\)
- \(5^{2}:5^{17}=5^{2-17}=5^{-15}=\frac{1}{5^{15}}\)
- \((\frac{1}{8})^7 : (\frac{1}{8})^7 = (\frac{1}{8})^{7-7}=(\frac{1}{8})^{0}=1\)
- \((-3)^7/ (-3)^4=(-3)^{7-4}=(-3)^{3}=-27\)
- \(5^{-20}: 5^{20}=5^{-20-20}=5^{-40}=\frac{1}{5^{40}}\)
Potęgowanie potęg
Przykłady na zastosowanie trzeciego wzoru:
- \((5^5)^5=5^{5\cdot 5}=5^{25}\)
- \((5^{-1})^2=5^{-1\cdot 2}=5^{-2}=\frac{1}{5^2}=\frac{1}{25}\)
Potęga iloczynu liczb
Przykłady na zastosowanie czwartego wzoru:
- \(3^2\cdot 2^2=(3\cdot 2)^2=6^2=36\)
- \(5^{-2}\cdot 2^{-2}=(5\cdot 2)^{-2}=10^{-2}=\frac{1}{100}\)
- \(100^{57}\cdot 0,01^{57}=(100\cdot 0,01)^{57}=1^{57}=1\)
Potęgowanie ułamków
Przykłady na zastosowanie piątego wzoru:
- \(4^2:2^2=(4:2)^2=2^2=4\)
- \(2^{-2}:4^{-2}=(2:4)^{-2}=(\frac{1}{2})^{-2}=2^2=4\)
- \(100^{5}:0,01^{5}=(100:0,01)^{5}=10000^{5}=(10^4)^5=10^{20}\)
- \((\frac{2}{5})^2=\frac{2^2}{5^2}=\frac{4}{25}\)
Inne
Przyjrzyjmy się następującemu przykładowi: \(5^6 \cdot 6^5\).
Ponieważ nie mamy tutaj takich samych podstaw ani wykładników potęgi, żaden ze wzorów działań na potęgach nie może być zastosowany.
Zadanie
Oblicz: \(5^7+5^5\).
Ponieważ mamy tutaj takie same podstawy, możemy skorzystać ze wzoru pierwszego, ale „w drugą stronę”, to znaczy:
\(5^7+5^5=5^{5+2}+5^5=5^2\cdot5^5+5^5=5^5(5^2+1) = 26\cdot 5^5\)
Potęgi liczby 10
Szczególną uwagę warto zwrócić na potęgi liczby 10. Zauważmy, że:
\(1=10^0\)
\(10=10^1\)
\(100=10^2\)
\(1000=10^3\)
\(10000=10^4\)
Uogólniając, potęga liczby \(10\) wskazuje „liczbę zer po jedynce”.
Zatem dla przykładu \(10^20\) oznacza liczbę z dwudziestoma zerami, czyli 100000000000000000000.
Warto jeszcze zwrócić uwagę na ujemne potęgi liczby 10. Zauważmy, że
\(0,1=10^{-1}\)
\(0,01=10^{-2}\)
\(0,001=10^{-3}\)
\(0,0001=10^{-4}\)
Uogólniając, potęga ujemna liczby \(10\) wskazuje „na którym miejscu po przecinku znajduje się jedynka”.
Zatem dla przykładu \(10^{-10}\) oznacza liczbę 0,0000000001.
Reasumując:
Zadania z rozwiązaniami

Zadanie nr 1.
Uprościć wyrażenie:
\(\Large \frac{6^{\frac{4}{3}}\cdot (\frac{3}{8})^{0,25}\cdot 2^{-0,(3)}\cdot (\frac{3}{2})^{\frac{3}{5}}}{2^{\frac{3}{20}}\cdot 3^{\frac{11}{60}}}\)

Zadanie nr 2.
Uprościć wyrażenie:
\(\Large \frac{(x^{\frac{1}{4}}+1)(x^{-\frac{1}{4}}-1)}{3x^{\frac{1}{4}}}-\frac{3}{2x^{\frac{3}{4}}}\)

Zadanie nr 3.
Uprościć wyrażenie:
\(W=[(a^3-x^2)^{\frac{1}{2}}-1][(a^3-x^2)^{\frac{1}{2}}+1]-a^3+\\+x^2+(a^3-x^2)^{-\frac{1}{2}}+a^{\frac{1}{2}}(a^2-\frac{x^2}{a})^{-\frac{1}{2}}+1\)

Zadanie nr 4.
Oblicz:
\(3^2\cdot 9^8\cdot (\frac{1}{3})^{-3}\cdot 27^{-5}\cdot 3^{\frac{1}{3}}\cdot 9^{\frac{1}{3}}\)

Zadanie nr 5.
Oblicz wartość wyrażenia:
\([(\frac{1}{5})^{-\frac{1}{2}}]^4+5\cdot 5^{-2}-(\frac{1}{5^3})^{-1}\)

Zadanie nr 6.
Oblicz wartość wyrażenia, korzystając z własności potęg:
\((5^{-\frac{1}{2}})^{5^{\frac{1}{3}}\cdot 25^{-\frac{2}{3}}}\)

Zadanie nr 7 — maturalne.
Dla każdej dodatniej liczby a iloraz \(\frac{a^{-2,6}}{a^{1,3}}\) jest równy:
A. \(a^{-3,9}\)
B. \(a^{-2}\)
C. \(a^{-1,3}\)
D. \(a^{1,3}\)

Zadanie nr 8 — maturalne.
Liczba \(5^8*16^{(-2)}\) jest równa
A. \((\frac{5}{2})^8\)
B. \((\frac{5}{8})^8\)
C. \(10^8\)
D. \(10\)

Zadanie nr 9 — maturalne.
Dane są liczby \(a=3,6⋅10^{-12}\) oraz \(b=2,4⋅10^{-20}\). Wtedy iloraz \(\frac{a}{b}\) jest równy:
- \(8,64⋅10^{−32}\)
- \(1,5⋅10^{−8}\)
- \(1,5⋅10^{8}\)
- \(8,64⋅10^{32}\)

Zadanie nr 10 — maturalne.
Liczba naturalna \(n=2^{14}\cdot 5^{15}\) w zapisie dziesiętnym ma
A. 14 cyfr
B. 15 cyfr
C. 16 cyfr
D. 30 cyfr

Zadanie nr 11 — maturalne.
Liczba \(\frac{2^{50}\cdot 3^{40}}{36^{10}}\) jest równa:
A. \(6^{70}\)
B. \(6^{45}\)
C. \(2^{30}\cdot 3^{20}\)
D. \(2^{10}\cdot 3^{20}\)

Zadanie nr 12 — maturalne.
Liczba \(100^5\cdot (0,1)^{-6}\) jest równa
A. \(10^{13}\)
B. \(10^{16}\)
C. \(10^{-1}\)
D. \(10^{-30}\)

Zadanie nr 13 — maturalne.
Liczba \(3^{2+\frac{1}{4}}\) jest równa
A. \(3^2\cdot \sqrt[4]{3}\)
B. \(\sqrt[4]{3^2}\)
C. \(3^2 +\sqrt[4]{3}\)
D. \(3^2\cdot \sqrt{3^4}\)

Zadanie nr 14 — maturalne.
Funkcja f określona jest wzorem \(f(x)=\frac{2x^3}{x^6+1}\) dla każdej liczby rzeczywistej \(x\). Wtedy \(f(-\sqrt[3]{3})\) jest równa:
A. \(-\frac{\sqrt[3]{9}}{2}\)
B. \(-\frac{3}{5}\)
C. \(\frac{3}{5}\)
D. \(\frac{3}{5}\)
Powiązane materiały
 Działania na potęgach
Działania na potęgach© medianauka.pl, 2009-01-19, A-144
Data aktualizacji artykułu: 2023-03-12

 Potęgowanie
Potęgowanie Potęgi
Potęgi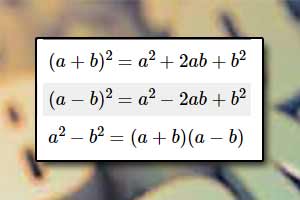 Wzory skróconego mnożenia
Wzory skróconego mnożenia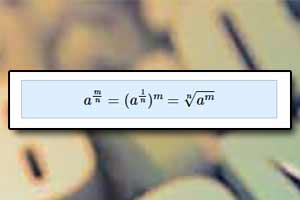 Potęga o wykładniku wymiernym
Potęga o wykładniku wymiernym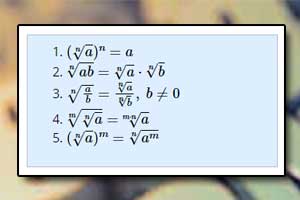 Działania na pierwiastkach
Działania na pierwiastkach Działania na potęgach — quiz
Działania na potęgach — quiz