Działania na pierwiastkach
Działania na potęgach i pierwiastkach rządzą się podobnymi prawami, ponieważ z definicji potęgi o wykładniku wymiernym wynika, że \(a^{\frac{m}{n}}=\sqrt[n]{a^m}\).
Wzory
Dla liczb naturalnych \(m\) i \(n\) oraz liczb rzeczywistych \(a\geq 0\) i \(b\geq 0\) prawdziwe są następujące wzory:
- \( (\sqrt[n]{a})^n=a\)
- \(\sqrt[n]{ab}=\sqrt[n]{a}\cdot \sqrt[n]{b}\)
- \( \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}},\ b\neq 0\)
- \( \sqrt[m]{\sqrt[n]{a}}=\sqrt[m\cdot n]{a}\)
- \( (\sqrt[n]{a})^m=\sqrt[n]{a^m} \)
Przykłady
Pierwiastek do potęgi n
Przykłady zastosowania pierwszego wzoru:
\((\sqrt[5]{77})^5=77\)
Powyższe wynika bezpośrednio z definicji pierwiastkowania jako działania odwrotnego do potęgowania.
Mnożenie pierwiastków
Przykłady zastosowania drugiego wzoru:
\(\sqrt[3]{54}=\sqrt[3]{27\cdot 2}=\sqrt[3]{27}\cdot \sqrt[3]{2}=3\sqrt[3]{2}\)
\( \sqrt[4]{32}=\sqrt[4]{16\cdot 2}=\sqrt[4]{16}\cdot \sqrt[4]{2}=2\sqrt[4]{2}\)
Dzielenie pierwiastków
Przykłady zastosowania trzeciego wzoru:
\(\sqrt[3]{\frac{3}{64}}=\frac{\sqrt[3]{3}}{\sqrt[3]{64}}=\frac{1}{4}\sqrt[3]{3} \)
\( \sqrt{\frac{9}{16}}=\frac{\sqrt{9}}{\sqrt{16}}=\frac{3}{4} \)
Pierwiastek z pierwiastka
Przykłady zastosowania czwartego wzoru:
\(\sqrt[4]{\sqrt[3]{12}}=\sqrt[4\cdot 3]{12}=\sqrt[12]{12}\)
\(\sqrt[4]{\sqrt{256}}=\sqrt[4\cdot 2]{256}=\sqrt[8]{256}=2\)
Potęgowanie pierwiastków
Przykłady zastosowania piątego wzoru:
\((\sqrt[3]{5})^2=\sqrt[3]{5^2}=\sqrt[3]{25} \)
\( (\sqrt[4]{3})^3=\sqrt[4]{3^3}=\sqrt[4]{27}\)
Pierwiastek a wartość bezwzględna
Dla każdej wartości a (a nie tylko dla dodatnich lub równych zero) pierwszy przytoczony tutaj wzór dla stopnia drugiego pierwiastka przyjmuje postać.
Zatem dla \(a\geq 0\) mamy \(\sqrt{a^2}=|a|=a\), natomiast dla \(a<0\) mamy \(\sqrt{a^2}=|a|=-a\).
Dodawanie pierwiastków
Działania sumy i różnicy pierwiastków nie nie zostały wyżej przedstawione. Jest tak dlatego, że nie ma takich wzorów dla dowolnych pierwiastków. Ich dodawanie lub odejmowanie nie zawsze da się przedstawić w taki sposób, żeby otrzymać wynik w postaci liczby bez konieczności zaokrąglania wyniku.
Dodając do siebie pierwiastki, można posłużyć się poniższym algorytmem:
- jeżeli jest to możliwe, wykonujemy pierwiastkowanie lub wyłączamy czynnik przed pierwiastek;
- jeżeli mamy jako składniki sumy pierwiastki tego samego stopnia z tej samej liczby, możemy dodać do siebie pierwiastki zgodnie ze wzorem \(m\sqrt{a}+n\sqrt{a}=(m+n)\sqrt{a}\).
Na przykład:
\(\sqrt{44}+3\sqrt{11}=2\sqrt{11}+3\sqrt{11}=5\sqrt{11}\)
\(\sqrt{4}+\sqrt{9}=2+3=5\)
W każdym innym przypadku pozostawiamy wynik w postaci sumy lub różnicy pierwiastków. Jest to dokładna reprezentacja liczby niewymiernej i nie ma potrzeby przedstawiać jej w inny sposób. Na przykład \(1+\sqrt{2}, \sqrt{3}-\sqrt{5}, 2\sqrt{2}-5\) pozostawiamy w takiej właśnie postaci.
Zadania z rozwiązaniami

Zadanie nr 4.
Oblicz wartość pierwiastka dla \(b>0\): \(\sqrt{\frac{a^6}{b^2}}\).

Zadanie nr 5.
Korzystając z własności działań na pierwiastkach lub potęgach, oblicz:
\(\sqrt{2}\cdot \sqrt[3]{2}\)

Zadanie nr 6.
Korzystając z własności działań na pierwiastkach lub potęgach oblicz: \(\sqrt{2}\cdot \sqrt[4]{4}:\sqrt[5]{16}\).

Zadanie nr 7.
Oblicz wartość wyrażenia: \(\sqrt{\sqrt[5]{\sqrt[4]{2^{48}}}}\)

Zadanie nr 8 — maturalne.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\sqrt[3]{-\frac{27}{16}}\cdot\sqrt[3]{2}\) jest równa
A. \((-\frac{3}{2})\)
B. \(\frac{3}{2}\)
C. \(\frac{2}{3}\)
D. \((-\frac{2}{3})\)

Zadanie nr 9 — maturalne.
Liczba \(\sqrt[3]{\frac{7}{3}}\cdot \sqrt[3]{\frac{81}{56}}\) jest równa:
- \(\frac{\sqrt{3}}{2}\)
- \(\frac{3}{2\sqrt[3]{21}}\)
- \(\frac{3}{2}\)
- \(\frac{9}{4}\)

Zadanie nr 10.
Dla jakiej wartości parametru \(x\) prawdziwa jest równość \(\sqrt{(x^2-2x+1)^2}=x^2-2x+1\)?
Powiązane materiały
Ćwiczenia, sprawdziany i quizy
© medianauka.pl, 2009-01-24, A-146
Data aktualizacji artykułu: 2023-03-22

 Pierwiastek arytmetyczny
Pierwiastek arytmetyczny Wyłączanie czynnika przed pierwiastek
Wyłączanie czynnika przed pierwiastek Usuwanie niewymierności z mianownika
Usuwanie niewymierności z mianownika Działania na potęgach
Działania na potęgach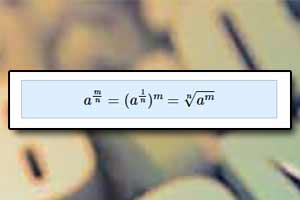 Potęga o wykładniku wymiernym
Potęga o wykładniku wymiernym Pierwiastkowanie
Pierwiastkowanie Pierwiastek — quiz
Pierwiastek — quiz Działania na pierwiastkach — quiz
Działania na pierwiastkach — quiz



