Oznaczenia i symbole matematyczne

W matematyce stosuje się wiele symboli. W poniższej tabeli zostały zestawione wszystkie symbole matematyczne stosowane w niniejszym kursie wraz z ich wyjaśnieniami.

SYMBOL	ZNACZENIE	PRZYKŁAD	OPIS PRZYKŁADU
Ø	zbiór pusty	-	-
N, Z₊	zbiór liczby naturalne	N={0,1,2,...}	-
N₀	zbiór liczb naturalnych z zerem	N₀={0,1,2,...}	N₀ jest równoważny zapisowi N
N₊	zbiór liczb naturalnych z wyłączeniem zera	N₊={1,2,3,...}	-
C, Z	zbiór liczb całkowitych	C={0,1,-1,2,-2,...}	-
W, Q	zbiór liczb wymiernych	-	-
ℵ₀	alef zero	-	-
$\overline{\overline{A}}$ lub \|A\|	moc zbioru A	\|A\|=2	Moc zbioru A jest równa 2
∈	należy do	a∈B	Element a należy do zbioru B
∉	nie należy do	a∉B	Element a nie należy do zbioru B
⊂	zawiera się	A⊂B	Zbiór A zawiera się w zbiorze B
⊄	nie zawiera się	A⊄B	Zbiór A nie zawiera się w zbiorze B
∪	suma zbiorów	A∪B={1,2}	Sumą zbiorów A i B jest zbiór {1,2}
\	różnica zbiorów	A\B={2}	Różnicą zbiorów A i B jest zbiór {2}
∩	iloczyn zbiorów	A∩B={1}	Iloczynem zbiorów A i B jest zbiór {1}
×	iloczyn kartezjański	A×B={(1,2),(2,1)}	Iloczynem kartezjańskim zbiorów A i B jest zbiór {(1,2),(2,1)}
~	negacja, zaprzeczenie	~p	Zaprzeczenie zdania p
∧	koniunkcja, iloczyn logiczny	p ∧ q	Iloczyn logiczny zdań p i q
∨	alternatywa, suma logiczna	p ∨ q	Suma logiczna zdań p i q
⇔	wtedy i tylko wtedy (równoważność zdań)	x-1=0 ⇔ x=1	x-1=0 wtedy i tylko wtedy, gdy x=1
⇒	implikacja, z ... wynika ...	p ⇒ q	Ze zdania p wynika q; Zdanie p implikuje zdanie q
	dla każdego x (kwantyfikatory)	[(x-1)²=x²-2x+1]	Dla każdego x spełniona jest równość (x-1)²=x²-2x+1
	istnieje takie x, że ... (kwantyfikatory)	(x-1=0)	Istnieje takie x, że x-1=0
=	równa się	x=5	x równa się 5
≠	jest różne	x≠5	x jest różne od 5
≈	znak przybliżenia	x≈5	x w przybliżeniu jest równe od 5
<	znak mniejszości	x<5	x jest mniejsze od 5
>	znak większości	x>5	x jest większe od 5
≤	znak mniejszości lub równości	x≤5	x jest mniejsze lub równe 5
≥	znak większości lub równości	x≥5	x jest większe lub równe 5
\|a\|	wartość bezwzględna (moduł) liczby a	\|-5\|=5	wartość bezwzględna z liczby -5 jest równa 5
+	plus (dodawanie, suma)	2+3=5	2 dodać 3 równa się 5
-	minus (odejmowanie, różnica)	2-3=-1	2 minus 3 równa się -1
·	mnożenie (iloczyn)	2·3=6, ab, 2x	2 razy 3 równa się 6, czasem znak ten pomijamy na przykład gdy mnożymy dwie zmienne lub liczbę przez niewiadomą
:,—,/	dzielenie (iloraz)	$6:3=\frac{6}{3}=6/3$	6 podzielić na trzy, iloraz liczb 6 i 3, sześć trzecich
aⁿ	potęgowanie	2³=8	2 do potęgi trzeciej jest równe 8
$\sqrt{a}$	pierwiastek kwadratowy (krótko: pierwiastek) z a	$\sqrt{4}=2$	pierwiastek z czterech jest równy 2
$\sqrt[n]{a}$	pierwiastek n-tego stopnia z liczby a	$\sqrt[3]{8}=2$	pierwiastek trzeciego stopnia z ośmiu jest równy 2
log_ba	logarytm przy podstawie b z a	log₂32=5	logarytm przy podstawie 2 z 32 jest równy 5
loga	logarytm dziesiętny (krótko: logarytm) z a	log100=2	logarytm ze 100 jest równy 2
lna	logarytm naturalny z a	lne=1	logarytm naturalny z e jest równy 1
exp x	funkcja wykładnicza e^x	exp(2x+1)=e^2x+1
!	silnia	3!=6	trzy silnia równa się sześć
(),<>,[],{}	nawiasy, kolejność wykonywania działań	(2+3)-(4-3)	działania wykonujemy najpierw w nawiasach
sin	sinus	sinx	sinus x
cos	cosinus (czytaj: kosinus)	cosx	cosinus x
tg	tangens	tgx	tangens x
ctg	cotangens (czytaj:kotangens)	ctgx	cotangens x
sec	secans (czytaj:sekans)	sec x	secans x
cosec	cosecans (czytaj:kosekans)	cosec x	cosecans x
arc sin	arcus sinus	arc sinx	arcus sinus x
arc cos	arcus cosinus	arc cosx	arcus cosinus x
arc tg	arcus tangens	arc tgx	arcus tangens x
arc ctg	arcus cotangens	arc ctgx	arcus cotangens x
⊥	jest prostopadłe	a ⊥ b	proste a i b są prostopadłe
$\parallel$	jest równoległe	a $\parallel$ b	proste a i b są równoległe
∢	kąt	∢ABC	kąt ABC
$\smile$	łuk	$\ \smile\\ AB$	łuk AB
°	stopień w mierze kątowej	5°	pięć stopni
′	minuta w mierze kątowej		pięć stopni i dwie minuty
′′	sekunda w mierze kątowej		pięć stopni, dwie minuty i dwadzieścia sekund
$\pi$	stała (liczba) pi	$\pi$ =3,14159...
e	stała(liczba) e - podstawa logarytmu naturalnego	e=2,71828...
$\gamma$	stała Eulera	$\gamma$ =0,57722...
∞	nieskończoność (liczba nieskończona)	-
$\lim-{n\to\infty} (a-n)$	granica ciągu a_n przy n dążącym do nieskończoności	-
$\sum-{i=1}^{n}$	suma, w której i zmienia się od 1 do n (symbol sigma)	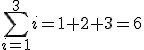$\sum-{i=1}^{3} {i}=1+2+3=6$
$\prod-{i=1}^{n}$	iloczyn, w którym i zmienia się od 1 do n (symbol pi)	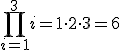$\prod-{i=1}^{3} {i}=1\cdot 2\cdot 3=6$
$\Delta$	przyrost	$\Delta x=x-2-x-1$	-
$',\ '',\ ''',\ ^{(n)}$	oznaczenie kolejnych pochodnych	$f'(x), f'''(x), f^{(5)}$	pochodna funkcji pierwszego, trzeciego i piątego rzędu
$\frac{d}{dx},\ \frac{d^2}{dx^2}$	oznaczenie kolejnych pochodnych	$\frac{dy}{dx},\ \frac{d^2y}{d^2x}$	pierwsza i druga pochodna funkcji y=f(x) po x
$\int$	całka nieoznaczona	$\int{xdx}$	całka funkcji f(x)=x po x
$\int{\int}$	całka podwójna	$\int{\int{xdx}}$	całka podwójna funkcji f(x)=x po x
$\int\limits-{a}^{b}$	całka oznaczona od dolnej granicy a do górnej granicy b	$\int\limits-{0}^{1}{xdx}$	całka oznaczona od 0 do 1 funkcji f(x)=x po x
$\vec{a}$	wektor a	-	-
$\vec{a}\circ \vec{b}$	iloczyn skalarny wektorów	-	-
$\vec{a}\times \vec{b}$	iloczyn wektorowy wektorów	-	-
%	procent	30%	30 procent
${n\choose k}$	symbol Newtona	-	-
∇²	laplasjan, operator Laplace'a

Grecki alfabet
Bardzo często w matematyce i fizyce stosuje się dla oznaczeń różnych wielkości litery alfabetu greckiego. Warto więc zapoznać się z nimi