Logarytm dziesiętny

Logarytm o podstawie 10 nazywamy logarytmem dziesiętnym.

$\log_{10}x=\log x$

Jeżeli więc nie podajemy podstawy logarytmu, mamy zawsze na myśli logarytm o podstawie 10.

Logarytm dziesiętny składa się z następujących składników:

cecha - jest to część całkowita logarytmu, to znaczy największa liczba całkowita nie większa od logarytmu, oznaczmy ją przez c (może być to liczba dodatnia, ujemna oraz zero),
mantysa - jest to różnica między logarytmem danej liczby, a cechą tego logarytmu, oznaczmy ją przez m (m spełnia warunek 0 ≤ m < 1).

Możemy więc zapisać, że $\log x=c+m$ .

Przykład

$\log 84=1+m_{1}$

W powyższym przykładzie wyznaczono cechę: ponieważ 10¹=10, a 10²=100 i 10<84<100, więc 1 jest cechą tego logarytmu, m₁ jest mantysą. Widać teraz, że logarytm ten jest większy od 1 i mniejszy od 2. Mantysy zwykle odczytujemy z tablic matematycznych.

A oto inne przykłady:

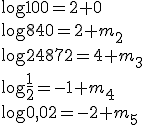
$\log 100=2+0\\ \log 840=2+m_{2}\\ \log 24872=4+m_{3}\\ \log{\frac{1}{2}}=-1+m_{4}\\ \log{0,02}=-2+m_{5}$