Symbol sigma (Σ)

Jeżeli dodajemy do siebie wiele składników i zauważamy pewną regułę, możemy do oznaczenia sumy stosować znak "sigma" (Σ).

Zamiast pisać 1+2+3+4+5+6+7+8+9 możemy napisać:

Przeanalizujmy ten zapis: Wprowadza się tutaj tak zwany indeks (wskaźnik) oznaczony literą "i", który zmienia się w odstępie co 1 dla każdego kolejnego składnika sumy od wartości zapisanej pod znakiem "sigma" do wartości zapisanej nad znakiem "sigma". W naszym przypadku dodajemy liczby różniące się o 1 począwszy od jedynki aż do 9, dlatego można było zastosować właśnie taką skróconą notację.

Próbując rozumować w drugą stronę (rozwinąć skrócony zapis) przyjmujemy początkową wartość indeksu (zapisaną pod znakiem "sigma") i wstawiamy tę wartość do wzoru przy znaku "sigma". Otrzymujemy pierwszy składnik sumy. Następnie zwiększamy wartość wskaźnika "i" o jeden i znów podstawiamy do wzoru przy znaku "sigma". Podstawiamy wskaźnik tak długo, aż przyjmie wartość zapisaną nad symbolem "sigma" (wówczas tę wartość ostatni raz podstawiamy do wzoru).

Powyższy zapis czytamy następująco: suma składników postaci "i" rozciągnięta na wskaźniki od 1 do 9 (lub krócej: suma po "i" od i=1 do 9).

Animacja

Zapis ten jest często stosowany w matematyce, warto więc przyjrzeć się innym przykładom:

Przykład

Suma	Spostrzeżenia	Skrócony zapis
5+6+7+8+9+...+1000	Kolejne składniki sumy różnią się o 1 i zmieniają się w zakresie od 5 do 1000
-1+0+1+2+3+4+5+...	Kolejne składniki sumy różnią się o 1 i zmieniają się w zakresie od -1 do nieskończoności.
...+(-2)+(-1)+0+1+2+3+...	Kolejne składniki sumy różnią się o 1 i zmieniają się w zakresie od minus nieskończoności do plus nieskończoności.
0+2+4+6+8+...	Kolejne składniki sumy różnią się o 2 i zmieniają się w zakresie od 0 do plus nieskończoności. Tutaj również można zastosować zapis "sigma", jeśli zauważymy, że 0+2+4+6+8+... = 0x2+1x2+2x2+3x2+4x2+... Teraz widzimy, że w każdym składniku sumy mamy stały czynnik 2 i wskaźnik (wyróżniony pogrubioną czcionką), który zmienia się od 0 do nieskończoności.
1+3+5+7+9+...	Kolejne składniki sumy różnią się o 2 i zmieniają się w zakresie od 1 do plus nieskończoności. Tutaj również można zastosować zapis "sigma", jeśli zauważymy, że 1+3+5+7+... = (0x2+1)+(1x2+1)+(2x2+1)+(3x2+1)+... Teraz widzimy, że w każdym składniku sumy występuje wskaźnik (wyróżniony pogrubioną czcionką), który zmienia się od 0 do nieskończoności.
a₁+a₂+a₃+...+a_n	Mamy tutaj sumę wyrazów ogólnych. Z łatwością można znaleźć wskaźnik, po którym można sumować (jest to indeks dolny wyrazu "a", który zmienia się od 1 do n).
1+8+27+64+125+...	Mamy tutaj sumę sześcianów kolejnych liczb naturalnych, a więc 1³+2³+3³+4³+5³+... . Wskaźnikiem, po którym można sumować jest podstawa potęgi.
(x+1)⁵+(x+2)⁶+(x+3)⁷+ ...	Mamy tutaj dwa wskaźniki, ponieważ zmienia się potęga oraz składnik sumy w nawiasie. Ponieważ wskaźniki te różnią się siebie o stałą wartość, można zastosować zapis tradycyjny, ale można także wprowadzić dwa wskaźniki i oraz j.
(1²+1³)+(2²+2³)+(3²+3³)+...	To bardziej skomplikowany przykład. Zauważmy, że w każdym nawiasie mamy sumę, którą można zapisać za pomocą symbolu sigma: , ale tutaj widzimy również kolejny wskaźnik (w każdym symbolu sigma: 1,2,3,...), możemy więc znów sumować po tym wskaźniku ("j")

Zadanie

Wykazać, że
sigma - przykład .
Aby wykazać, że stałą wartość można wyłączyć przed znak "sigma", wystarczy rozpisać sumę, wyłączyć liczbę 2 przed nawias i dla sumy w nawiasie zastosować symbol "sigma":

Zadanie

Oblicz:

sigma - przykład .

Rozwiązanie:

Zadania z rozwiązaniami

Zadania związane z tematem:
Symbol sigma

Zadanie - symbol sigma, zastosowanie symbolu sigma
Oblicz:
a) $\sum_{i=-2}^{2}\frac{i}{i+4}$
b) $\sum_{i=1}^{4}i^i$
c) $\sum_{i=1}^{5}(i-5)$

Pokaż rozwiązanie zadania

Zadanie - zastosowanie symbolu sigma
Zapisać sumę 6+18+54+162+486 za pomocą symbolu "Σ".

Pokaż rozwiązanie zadania

Zadanie - obliczenia sumy i iloczynu
Oblicz: $\sum_{j=1}^{3}\prod_{i=1}^{5}ij$

Pokaż rozwiązanie zadania

Inne zagadnienia z tej lekcji

Suma
Dodawanie (suma) jest jednym z czterech podstawowych działań arytmetycznych. Symbolem tego działania jest + (plus).

Dodawanie pisemne
Dodawanie pisemne - procedura, przykłady, gra edukacyjna, kalkulator i quizy

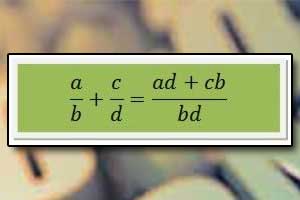Dodawanie ułamków zwykłych
Dodawanie ułamków odbywa się poprzez sprowadzenie ich do wspólnego mianownika.

Test wiedzy
Sprawdź swoje umiejętności z materiału zawartego w tej lekcji.