Funkcja wykładnicza

Funkcja wykładnicza jest to funkcja postaci:

\(y=a^x, a>0, a\in \mathbb{R}\)

W niektórych kursach matematyki w definicji funkcji wykładniczej pomija się przypadek, w którym \(a=1\). Wówczas mamy do czynienia z funkcją stałą \(y=1\).

Funkcja wykładnicza a logarytmiczna

Funkcja wykładnicza \(y=a^x\) jest funkcją odwrotną do funkcji logarytmicznej \(y=\log_{a}{x}\).

Funkcja eksponencjalna

Szczególnym przypadkiem funkcji wykładniczej jest funkcja eksponencjalna, która w podstawie potęgi ma podstawę logarytmu naturalnego — liczbę \(e\) (liczba Eulera).

\(f(x)=e^x\)

Przykłady

A oto przykłady funkcji wykładniczych:

\(y=2^x\)
\(f(x)=(\frac{3}{7})^x\)
\(y=(1+\sqrt{2}+\sqrt{3})^x\)
\(y=1^x=1\)

Własności funkcji wykładniczej

Dziedzina funkcji wykładniczej: dziedziną funkcji wykładniczej jest zbiór liczb rzeczywistych \(\mathbb{R}\).
Zbiór wartości funkcji wykładniczej: przeciwdziedziną funkcji wykładniczej jest zbiór liczb rzeczywistych dodatnich \(\mathbb{R}_+\).
Monotoniczność funkcji wykładniczej: funkcja wykładnicza jest rosnąca dla \(a>1\), malejąca, gdy \(0<a<1\) oraz stała, gdy \(a=1\).
Funkcja wykładnicza to jedyna funkcja ciągła, której dziedziną jest cały zbiór liczb rzeczywistych i ma tę własność, że dla dowolnych argumentów \(x_1, x_2\) spełniona jest zależność: \(f(x_1+x_2)=f(x_1)\cdot f(x_2)\).

W dalszej części lekcji omawiamy wykres funkcji wykładniczej.

Pytania

Czy funkcja wykładnicza jest funkcją potęgową?

Nie. Funkcja wykładnicza charakteryzuje się tym, że niewiadoma znajduje się w wykładniku potęgi, a w funkcji potęgowej niewiadoma znajduje się w podstawie potęgi. To dwie różne funkcje o różnych własnościach.

Jaka jest pochodna funkcji wykładniczej?

Pochodna funkcji wykładniczej jest określona dla \(a\in \mathbb{R}_+\) i jest równa \((a^x)'=a^x\cdot \ln{a}\).

Ciekawym przypadkiem jest pochodna funkcji eksponencjalnej. Otóż \((e^x)'=e^x\).

Zadania z rozwiązaniami

Zadanie nr 1.

Wykazać, że ciąg \(a_n=(\sqrt{2})^n\) jest ciągiem geometrycznym.

Pokaż rozwiązanie zadania.

Zadanie nr 2 — maturalne.

Na rysunku przedstawiono fragment wykresu funkcji wykładniczej \(f\) określonej wzorem \(f(x)=a^x\). Punkt \(A=(1,2)\) należy do tego wykresu funkcji.

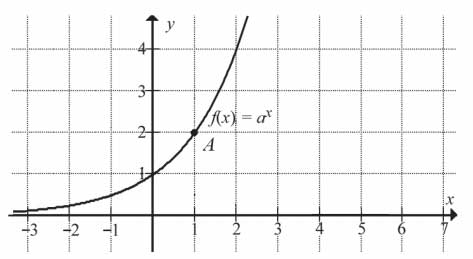
Rysunek do zadania

Podstawa potęgi \(a\) jest równa:

A. \(-\frac{1}{2}\)

B. \(1\frac{1}{2}\)

C. -2

D. 2

Pokaż rozwiązanie zadania.

Zadanie nr 3 — maturalne.

Do wykresu funkcji wykładniczej, określonej dla każdej liczby rzeczywistej \(x\) wzorem \(f(x)=a^x\) (gdzie \(a>0\) i \(a\neq 1\), należy punkt \(P=(2,9)\). Oblicz a i zapisz zbiór wartości funkcji g, określonej wzorem \(g(x)=f(x)−2\).

Pokaż rozwiązanie zadania.

Powiązane materiały

Wykres funkcji wykładniczej

Funkcja wykładnicza

Funkcja potęgowa

Funkcja logarytmiczna

Ćwiczenia

Funkcja wykładnicza