Wykres funkcji wykładniczej
Wykres funkcji wykładniczej nosi nazwę krzywej wykładniczej. Krzywa wykładnicza ma różny kształt, w zależności od wartości argumentu funkcji.
Przykłady
Narysuj wykres funkcji wykładniczej \(y=2^x\), \(y=(\frac{1}{2})^x\) oraz \(y=1^x\).
Sporządzamy najpierw tabelkę zmienności wszystkich funkcji:
| \(x\) | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| \(y=2^x\) | \(\frac{1}{4}\) | \(\frac{1}{2}\) | 1 | 2 | 4 |
| \(y=(\frac{1}{2})^x\) | 4 | 2 | 1 | \(\frac{1}{2}\) | \(\frac{1}{4}\) |
| \(y=1^x\) | 1 | 1 | 1 | 1 | 1 |
Szkicujemy wykresy:
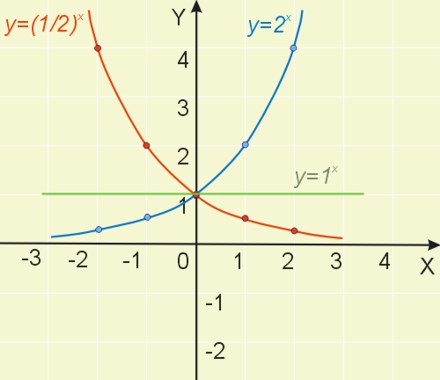
Cechą charakterystyczną wykresu funkcji wykładniczej jest to, że zawsze przechodzi przez punkt \((0,1)\).
Wykres funkcji wykładniczej online
Poniższa symulacja ilustruje zachowanie się wykresu w zależności od wartości podstawy potęgi. Ustawienia można zmieniać za pomocą suwaka.
Funkcja w postaci y = ax, czyli y = 2x
a 2Przekształcenia wykresu funkcji wykładniczej
Wzór funkcji \(f(x)\) przesuniętej o wektor \(\vec{v}=[p,q]\) ma postać \(y=f(x-p)+q\), czyli w przypadku funkcji wykładniczej:
Przykłady
- Aby narysować wykres funkcji \(y=3^{x-5}\), wystarczy przesunąć wykres funkcji \(y=3^x\) o 5 jednostek w prawo (wzdłuż osi Ox).
- Aby narysować wykres funkcji \(y=3^{x+1}\), wystarczy przesunąć wykres funkcji \(y=3^x\) o 1 jednostkę w lewo (w stronę przeciwną do osi Ox).
- Aby narysować wykres funkcji \(y=3^{x}+5\), wystarczy przesunąć wykres funkcji \(y=3^x\) o 5 jednostek w górę (wzdłuż osi Oy).
- Aby narysować wykres funkcji \(y=3^{x+5}+5\), wystarczy przesunąć wykres funkcji \(y=3^x\) o wektor \(\vec{v}=[-5,5]\).
Zadania z rozwiązaniami
Zadanie nr 3 — maturalne.
Na rysunku przedstawiono fragment wykresu funkcji wykładniczej \(f\) określonej wzorem \(f(x)=a^x\). Punkt \(A=(1,2)\) należy do tego wykresu funkcji.
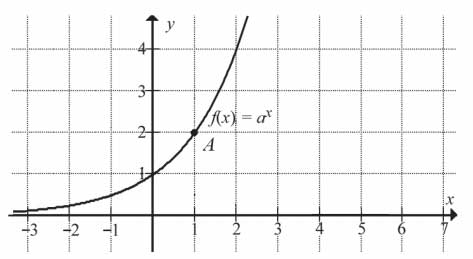
Podstawa potęgi \(a\) jest równa:
A. \(-\frac{1}{2}\)
B. \(1\frac{1}{2}\)
C. -2
D. 2
Inne zagadnienia z tej lekcji
Funkcja wykładnicza
Funkcja wykładnicza© medianauka.pl, 2010-10-10, A-384
Data aktualizacji artykułu: 2023-04-27