Procent

Obliczeniami procentowymi posługujemy się nader często w życiu codziennym. Pojęcia „procent” używamy w mowie potocznej, statystyce, bankowości, na giełdzie, praktycznie wszędzie tam, gdzie mówimy o pewnej części ilości. Procenty znajdziemy na etykietach towarów, w grach komputerowych, bankach, a nawet w wynikach badań lekarskich.

Co to jest procent?

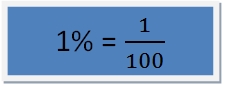
Procent to jedna setna część pewnej wielkości.

Kiedy mówimy o procencie lub oprocentowaniu, to zawsze odnosimy się do pewnej liczby. Mówiąc, że cena wzrosła o 5%, odnosimy się do ceny wyjściowej, a twierdząc, że 51% ludzi w Polsce to kobiety, odnosimy się do liczby wszystkich ludzi w kraju itd.

Skoro 1% oznacza 1/100, to co oznacza 2%? Oczywiście 2/100, 3% oznacza 3/100 i tak dalej.

Podsumowując:

Zamiana procentu na liczbę

Aby zamienić p% na liczbę, należy podzielić liczbę p przez 100.

Przykłady

\(5\%=5:100=\frac{5}{100}=\frac{1}{20}\)
\(33\%=33:100=\frac{33}{100}\)
\( \frac{1}{2}\%=\frac{1}{2}:100=\frac{1}{200}\)
\(100\%=100:100=1\)
\(1000\%=1000:100=10\)
\( 0,1\%=0,1:100=0,001\)
\(p\%=p:100=\frac{p}{100}\)

Bardzo często przydaje się także odwrotna do powyższej operacja, a mianowicie zamiana liczby na procent.

Zamiana liczby na procent

Aby zamienić liczbę na procent, należy pomnożyć liczbę przez 100 i wynik oznaczyć symbolem "%".

Przykłady

Oto przykłady jak obliczyć ile to procent, gdy dana jest liczba.

\(\frac{1}{5}=(\frac{1}{5}\cdot 100)\%=20\%\)
\(1=(1\cdot 100)\%=100\%\)
\(\frac{1}{2}=(\frac{1}{2}\cdot 100)\%=50\%\)
\(0,04=(0,04\cdot 100)\%=4\%\)
\(\frac{2}{3}=(\frac{2}{3}\cdot 100)\%=\frac{200}{3}\%=66\frac{2}{3}\%\)
\(2\frac{3}{5}=\frac{13}{5}=(\frac{13}{5}\cdot 100)\%=\frac{1300}{5}\%=260\%\)
\(p=(p\cdot 100)\%=100p\%\)

Kalkulator procentów

Kalkulator — procent z liczby
Nasz kalkulator online oblicza procent podanej liczby.

Wpisz dane:
Procent % z liczby x:

Rozwiązanie:

Obliczanie procentów

Przedstawiamy tu różne rodzaje obliczeń na procentach. Zachęcamy do przeprowadzenia quizu i rozwiązania naszych zadań. Obliczenia procentowe spotykamy w życiu niemalże na każdym kroku, nawet w grach komputerowych. Warto posługiwać się nimi biegle.

Obliczanie procentu danej liczby

Jak obliczyć procent z liczby? Aby obliczyć p% danej liczby a, wystarczy pomnożyć liczbę a przez ułamek p/100. Obliczanie procentu z liczby możemy ująć następująco:

\(p\%\quad liczby\quad a,\quad to \quad \frac{p}{100}\cdot a = \frac{p\cdot a}{100}\)

Powyższa zasada pozwoli nam obliczyć procent z kwoty, a także procent z ceny towaru i dowolnej innej wartości.

Przykłady

Oblicz procent z liczby:

33% liczby 100, to \(\frac{33}{100}\cdot 100=33\)
20% liczby 5, to \(\frac{20}{100}\cdot 5 = \frac{1}{5}\cdot 5=1\)
15% liczby 20, to \(\frac{15}{100}\cdot 20 = \frac{3}{20}\cdot 20=3\)
0,2% liczby 30, to \(\frac{\frac{2}{10}}{100}\cdot 30 = \frac{2}{1000}\cdot 30 = \frac{60}{1000}=\frac{6}{100}=0,06\)

Zadanie 1

Pan Kowalski włożył do banku 4000 zł na roczną lokatę 6%. Jaką kwotę po roku otrzyma z banku pan Kowalski?

Obliczamy najpierw odsetki: \(\frac{6}{100}\cdot 4000=\frac{6\cdot 4000}{100}=240\).

Zatem pan Kowalski po roku czasu otrzyma swój wkład oraz odsetki, a więc: 4000 zł + 240 zł = 4240 zł.

Odpowiedź: Pan Kowalski po roku czasu otrzyma z banku 4240 zł.

Zadanie 2

Pan Kowalski włożył do banku 4000 zł na miesięczną lokatę o oprocentowaniu 6% w skali roku. Jaką kwotę po miesiącu otrzyma z banku pan Kowalski? A jaką kwotę pan Kowalski otrzyma, po przelaniu wszystkich środków na kolejną miesięczną lokatę na tych samych warunkach?

Obliczamy najpierw odsetki w skali roku: \(\frac{6}{100}\cdot 4000=\frac{6\cdot 4000}{100}=240\), a następnie obliczamy wartość odsetek w skali miesiąca (jeden miesiąc, to 1/12 roku): \(\frac{1}{12}\cdot 240=20\)

Zatem pan Kowalski po roku czasu otrzyma swój wkład oraz odsetki, a więc: 4000 zł + 20 zł = 4020 zł

Kwota kapitału wynosi teraz 4020 zł, a więc powtarzamy powyższe rachunki dla tej kwoty:
Obliczamy najpierw odsetki w skali roku: \(\frac{6}{100}\cdot 4020=\frac{6\cdot 4020}{100}=241,2\), a następnie obliczamy wartość odsetek w skali miesiąca (jeden miesiąc, to 1/12 roku): \(\frac{1}{12}\cdot 241,2 = 20,1\).

Odpowiedź: Zatem pan Kowalski po miesiącu czasu otrzyma swój wkład oraz odsetki, a więc: 4000 zł + 20 zł = 4020 zł, natomiast po wyjęciu środków z kolejnej lokaty pan Kowalski otrzyma kwotę kapitału i odsetki 4020 zł + 20,10 zł = 4040,10 zł

Ciekawostki

Jeśli miałbyś do wyboru włożyć do banku 10 000 zł do banku na roczną lokatę o oprocentowaniu 5% w skali roku albo na 12 lokat jednomiesięcznych o oprocentowaniu 4,9 %, jaką opcję byś wybrał w celu uzyskania najlepszych zysków?

Wydawałoby się, że w obu przypadkach przechowujemy w banku pieniądze przez ten sam okres czasu, w drugim przypadku mamy mniejsze oprocentowanie, więc odsetki powinny być większe dla lokaty rocznej. Jednak w tym przypadku tak wcale nie jest! W przypadku 12 lokat miesięcznych odsetki doliczane są za każdym razem do kwoty kapitału (kwoty wyjściowej), a więc obliczamy co miesiąc odsetki od coraz to większej kwoty. W przypadku rocznej lokaty otrzymałbyś 500 zł odsetek, w przypadku 12 lokat miesięcznych ponad 501 zł. Policz sam.

Zadanie 3

Straganiarz sprzedawał jabłka po 5 zł za 1 kg. Ponieważ rano sprzedawał bardzo dużo towaru podniósł cenę jabłek o 5%. Jednak pod koniec dnia, kiedy było już mniej klientów, obniżył cenę jabłek o 5%. Ile kosztowały jabłka pod koniec dnia?

Po podwyżce jabłka kosztowały \(5PLN + \frac{5}{100}\cdot 5PLN=5,25 PLN\).

Po obniżce jabłka kosztowały \(5,25PLN - \frac{5}{100}\cdot 5,25PLN=4,99 PLN\).

Odpowiedź: Pod koniec dnia jabłka kosztowały 4,99 zł.

W powyższym zadaniu mamy do czynienia z ciekawym przypadkiem. Dlaczego po podwyżce ceny o 5% i obniżce o 5% nie otrzymaliśmy ceny wyjściowej? Bo obliczaliśmy procent od różnych wartości ceny (5% z 5zł to nie to samo, co 5% z 5,25%).

Znajdowanie liczby na podstawie
danego jej procentu

Jeżeli liczba a stanowi p% liczby b, to:

\(b=\frac{a\cdot 100}{p}\)

Przykłady

5 stanowi 10% pewnej liczby. Jaka to liczba?

Korzystamy z powyższego wzoru i otrzymujemy: \(\frac{5\cdot 100}{10}=50\).

Zadanie 4

Pan Nowak otrzymał po roku oszczędzania 350 zł odsetek z lokaty oprocentowanej w wysokości 7% w skali roku. Jaka kwota była na lokacie?

Korzystamy z powyższego wzoru: \(\frac{350\cdot 100}{7}=5000\).

Odpowiedź: Pan Nowak miał na lokacie rocznej 5000 zł.

A co zrobić, gdy zapomnimy wzoru? Wówczas wystarczy pamiętać co oznacza procent, uświadomić sobie jakiej wielkości szukamy, oznaczyć ją przez x i ułożyć oraz rozwiązać równanie. Dla przykładu dla powyższego zadania można ułożyć następujące równanie: \(7\%\cdot x=350\), gdzie x oznacza kwotę od jakiej obliczane są odsetki, czyli kwotę kapitału. Mamy dalej:

\(\frac{7}{100}x=350 /\cdot 100\)

\(7x=35000 /:7\)

\(x=5000\)

Obliczanie, jaki procent jednej liczby stanowi druga liczba

Korzystamy z następującego wzoru:

Liczba b stanowi \((\frac{b}{a}\cdot 100)\%\) liczby a

Przykłady

Jaki procent liczby 40 stanowi liczba 5?

Korzystamy z powyższego wzoru i otrzymujemy: \((\frac{5}{40}\cdot 100)\%=12,5\%\)

Zadanie

Pan Nowak otrzymał po roku oszczędzania 200 zł odsetek od 5000 zł, jakie włożył na roczną lokatę. Jak była oprocentowana lokata?

Korzystamy z powyższego wzoru: \((\frac{200}{5000}\cdot 100)\%=4\%\)

Odpowiedź: Oprocentowanie lokaty wynosiło 4% w skali roku.

A co zrobić, gdy zapomnimy wzoru? Wówczas wystarczy pamiętać co oznacza procent, uświadomić sobie jakiej wielkości szukamy, oznaczyć ją przez x i ułożyć oraz rozwiązać równanie. Dla przykładu dla powyższego zadania można ułożyć następujące równanie: \(5000\cdot x\%=200\), gdzie x oznacza stopę oprocentowania. Mamy dalej:

\(x\cdot \frac{1}{100}=\frac{200}{5000} /\cdot 100\)

\(x=4\)

Zamiana ułamków na procenty

Aby zamienić ułamek na procenty wystarczy go pomnożyć przez 100%.

Przykłady

Zamień ułamki na procenty:

\(\frac{1}{5}=\frac{1}{5}\cdot 100\%=\frac{100}{5}\%=20\%\)
\(0,02=0,02\cdot 100\%=2\%\)
\(\frac{4}{3}=\frac{4}{3}\cdot 100\%=\frac{400}{3}\%=133,(3)\%\)

Pytania

Jak obliczyć procent na kalkulatorze?

Najprostszą metodą obliczenia procentu z liczby przy pomocy kalkulatora, jest w pierwszej kolejności zamiana procentu na ułamek dziesiętny i pomnożenie go przez konkretną liczbę. Dla przykładu, aby obliczyć 10% z liczby 20, wprowadzamy do kalkulatora 0,1×20, uzyskując w ten sposób wynik 2.

Jeżeli mamy klawisz procentu na kalkulatorze wystarczy wprowadzić działanie 20×10% i nacisnąć znak równości.

Jak obliczyć procent w Excelu?

Jeżeli chcemy obliczyć ile wynosi procent z wybranej liczby w Excelu, wpisujemy do komórki znak równania (=) i definiujemy podobne działanie, jak w przypadku zwykłego kalkulatora.

Przykładowo chcąc uzyskać 10% z liczby 20, możemy wpisać do komórki formułę =20*0,1, albo możemy też użyć znaku procentu: =20*10%.

Jak zapisać procenty w postaci ułamków dziesiętnych?

Aby zamienić procenty na ułamek dziesiętny, wystarczy przesunąć przecinek o dwa miejsca w lewo. Na przykład 10% = 0,01, 15% = 0,15, 1% = 0,01.

Zadania z rozwiązaniami

Zadanie nr 1.

Książka, która początkowo kosztowała 40 zł po rabacie kosztowała 35 zł. O ile procent obniżono cenę książki?

Procent

Co to jest procent?

Zamiana procentu na liczbę

Przykłady

Zamiana liczby na procent

Przykłady

Kalkulator procentów

Obliczanie procentów

Obliczanie procentu danej liczby

Przykłady

Zadanie 1

Zadanie 2

Ciekawostki

Zadanie 3

Znajdowanie liczby na podstawiedanego jej procentu

Przykłady

Zadanie 4

Obliczanie, jaki procent jednej liczby stanowi druga liczba

Przykłady

Zadanie

Zamiana ułamków na procenty

Przykłady

Pytania

Zadania z rozwiązaniami

Powiązane materiały

Znajdowanie liczby na podstawie
danego jej procentu