Iloczyn skalarny
Co to jest iloczyn skalarny wektorów? Mnożenie skalarne wektorów nie jest jedynym działaniem iloczynu na wektorach. Pamiętajmy, że jest jeszcze mnożenie wektora przez skalar. Jest także iloczyn wektorowy.
Istnieją dwa pojęcia iloczynu wektorów. Wynikiem jednego iloczynu jest liczba (skalar) i iloczyn ten nazywamy iloczynem skalarnym. Wynikiem drugiego iloczynu jest wektor — iloczyn ten nazywamy iloczynem wektorowym. W niniejszym artykule zajmiemy się tylko iloczynem skalarnym.
Definicja
Iloczyn skalarny dwóch wektorów \(\vec{a}\) i \(\vec{b}\) jest to liczba równa iloczynowi modułów (długości) tych wektorów i cosinusa kąta między nimi w przypadku, gdy są to wektory niezerowe i równa zeru, gdy jeden lub drugi wektor jest wektorem zerowym.
Iloczyn skalarny oznaczamy następująco:
Powyższy wzór na iloczyn skalarny wykorzystamy w przykładowym zadaniu:
Przykład 1
Dla przykładu obliczymy iloczyn wektorów \(\vec{a}=[1,2]\) i \(\vec{b}=[-4,2]\), jeżeli wiadomo, że kąt między tymi wektorami ma miarę 90°.
Obliczamy najpierw moduły wektorów:
\(|\vec{a}|=a=\sqrt{1^2+2^2}=\sqrt{5}\)
\(\vec{b}|=b=\sqrt{(-4)^2+2^2}=\sqrt{16+4}=\sqrt{20}=2\sqrt{5}\)\)
Obliczamy iloczyn skalarny:
\(\vec{a}\circ \vec{b}=ab\cdot cos{(\vec{a}, \vec{b})}=\)
\(=\sqrt{5} \cdot 2\sqrt{5}\cdot \cos{90^o}=10\cdot 0 = 0\)
Twierdzenie 1
Iloczyn skalarny dwóch wektorów równa się sumie iloczynów równoimiennych współrzędnych tych wektorów:
Przykład 2
Zastosujemy powyższe twierdzenie do wyznaczenia iloczynu skalarnego wektorów z przykładu pierwszego:
\(\vec{a}\circ \vec{b}=1\cdot (-4)+2\cdot2=4-4=0\)
Własności iloczynu skalarnego
Oto wybrane własności iloczynu skalarnego:
- Iloczyn skalarny jest przemienny, tzn. \(\vec{a}\circ \vec{b}=\vec{b}\circ \vec{a}\).
- Iloczyn skalarny jest łączny względem mnożenia przez liczbę, tzn. \((k\vec{a})\circ \vec{b}=k(\vec{a}\circ \vec{b})\).
- Iloczyn skalarny jest rozdzielny względem dodawania wektorów, tzn. \((\vec{a}+\vec{b})\circ \vec{c}=\vec{a}\circ \vec{c}+\vec{b}\circ \vec{c}\).
- Iloczyn skalarny jest równy zeru, gdy jeden lub drugi z wektorów jest wektorem zerowym lub wektory są prostopadłe.
- Iloczyn skalarny wektora przez ten sam wektor jest równy kwadratowi modułu tego wektora: \(\vec{a}\circ \vec{a}=a^2\).
- Jeśli \(\vec{i}, \vec{j}\) są wersorami prostokątnego układu kartezjańskiego, to: \(\vec{i}\circ \vec{i}=1\), \(\vec{j}\circ \vec{j}=1\), \(\vec{i}\circ \vec{j}=0\).
Zastosowanie iloczynu skalarnego
Iloczyn skalarny ma dość szerokie zastosowanie w matematyce i fizyce. Tutaj skupimy się na zastosowaniu iloczynu skalarnego wektorów w geometrii.
Prostopadłość wektorów
Kiedy wektory są prostopadłe do siebie?
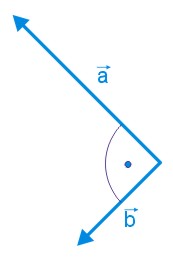
Twierdzenie 2
Jeśli dwa niezerowe wektory są prostopadłe, to ich iloczyn skalarny jest równy zeru.
Twierdzenie 3
Jeśli iloczyn skalarny dwóch wektorów jest równy zeru, to co najmniej jeden z nich jest wektorem zerowym lub wektory są prostopadłe
Równoległość wektorów
Kiedy dwa wektory są równoległe do siebie?
Twierdzenie 4
Jeżeli dwa niezerowe wektory są równoległe, to wyznacznik tych wektorów jest równy zeru:
\(\begin{vmatrix} a_x&a_y\\b_x&b_y \end{vmatrix}=a_xb_y-a_yb_x=0\)
Twierdzenie 5
Jeśli wyznacznik dwóch wektorów jest równy zeru, to albo co najmniej jeden z tych wektorów jest wektorem zerowym albo wektory są równoległe.
Przykład 3
Sprawdzimy, czy wektory \(\vec{a}=[1,3]\) i \(\vec{b}=[-2,-6]\) są równoległe. W tym celu obliczamy wyznacznik wektorów:
\(\begin{vmatrix} a_x&a_y\\b_x&b_y \end{vmatrix}=\begin{vmatrix} 1&3\\-2&-6 \end{vmatrix}=1\cdot (-6)-3\cdot(-2)=-6+6=0\)
Ponieważ wyznacznik wektorów niezerowych jest równy zero, wektory te są równoległe.
Pole równoległoboku i pole trójkąta
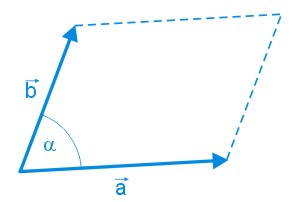
Twierdzenie 6
Pole \(P\) równoległoboku wyznaczonego przez dwa niezerowe wektory zaczepione we wspólnym początku jest równe modułowi wyznacznika \(W\) tych wektorów.
\(W=\begin{vmatrix} a_x&a_y\\b_x&b_y \end{vmatrix}=a_xb_y-a_yb_x\)
\(P=|W|\)
Twierdzenie 7
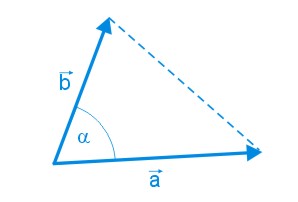
Pole trójkąta wyznaczonego przez dwa niezerowe wektory zaczepione we wspólnym początku jest równe połowie modułu wyznacznika tych wektorów.
\(W=\begin{vmatrix} a_x&a_y\\b_x&b_y \end{vmatrix}=a_xb_y-a_yb_x\)
\(P=\frac{1}{2}|W|\)
Przykład 4
Wyznaczyć pole trójkąta wyznaczonego przez wektory \([-1,1]\) i \([4,3]\).
Korzystamy z powyższego twierdzenia i obliczamy wyznacznik wektorów:
\(W=\begin{vmatrix} -1&1\\4&3 \end{vmatrix}=(-1)\cdot 3-1\cdot 4=-3-4=-7\)
\(P=|-7|=7\)
Zadania z rozwiązaniami
Zadanie nr 1.
Wektory \(\vec{a}=[1,2], \vec{b}=[-3,4]\) wyznaczają trójkąt. Obliczyć jego pole.
Zadanie nr 2.
Zbadać, czy wektory \(\vec{a}=[4,8], \vec{b}=[2,-1]\) są prostopadłe.
Zadanie nr 3.
Jaki kąt tworzą ze sobą wektory \(\vec{a}, \vec{b}\), jeżeli ich iloczyn skalarny jest równy \(1\), a długości tych wektorów są równe odpowiednio \(2\) i \(1\)?
Zadanie nr 4.
Dany jest wektor \(\vec{a}=[4,-5]\). Oblicz \(\vec{a}\circ 2\vec{a}\).
Zadanie nr 5.
Dane są wektory \(\vec{a}=2\vec{i}-4\vec{j}, \vec{b}=2\vec{i}+3\vec{j}\). Oblicz \(\vec{a}\circ \vec{b}\).
Zadanie nr 6.
Czy trójkąt wyznaczony przez wektory \(\vec{a}=[-2,4], \vec{b}=[3,1]\) jest trójkątem prostokątnym?
Zadanie nr 7.
Zbadać, czy wektory \(\vec{a}=[12,24], \vec{b}=[-3,-6]\) są równoległe.
Zadanie nr 8.
Dla jakiej wartości parametru \(m\) wektory \(\vec{a}=[2,-3], \vec{b}=[5,3m]\) są równoległe.
Zadanie nr 9.
Dla jakiej wartości parametru \(m\) wektory \(\vec{a}=[m,3], \vec{b}=[4,-2m+1]\) są prostopadłe?
Zadanie nr 10.
Dany jest wektor \(\vec{AB}=[2,5]\) zaczepiony w punkcie \(A=(1,1)\). Znaleźć taki punkt \(C\), leżący na prostej \(y=2\), że pole trójkąta \(ABC\) jest równe 10.
Zadanie nr 11.
Oblicz pole rombu \(ABCD\), jeżeli wiadomo, że \(A=(2,0), B=(3,2), C=(2,4), D=(1,2)\).
Zadanie nr 12.
Obliczyć pole równoległoboku \(ABCD\), jeżeli wiadomo, że \(A=(1,1), B=(5,1), C=(7,3), D=(3,3)\).
Powiązane materiały
Wektor
Długość wektora
Współrzędne wektora
Mnożenie wektora przez liczbę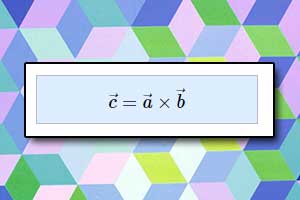
Iloczyn wektorowy
Reguła śruby prawoskrętnej
Pojęcie wektora
Iloczyn skalarny wektorów© medianauka.pl, 2010-12-12, A-1052
Data aktualizacji artykułu: 2023-07-11