Reguła śruby prawoskrętnej

Reguła ta określa zwrot wektora będącego iloczynem wektorowym dwóch wektorów.

Jeżeli dany jest iloczyn wektorowy \(\vec{c}=\vec{a}\times \vec{b}\), to zwrot wektora \(\vec{c}\) ustalamy następująco:

1. "Kręcimy" pierwszym wektorem z iloczynu wektorowego (tutaj \(\vec{a}\)) w kierunku drugiego (tutaj \(\vec{b}\)) w płaszczyźnie obu wektorów. Pamiętaj, że kolejność wektorów jest istotna!
2. Następnie wyobrażamy sobie prostopadle do płaszczyzny wektorów \(\vec{a}\) i \(\vec{b}\) śrubę prawoskrętną i kręcimy nią w kierunku, w jakim obracaliśmy pierwszy z wektorów iloczynu wektorowego.
3. Jeżeli śrubę wykręcamy (śruba porusza się ku górze), to zwrot wektora \(\vec{c}\) obieramy do góry.
4. Jeżeli śrubę wkręcamy (śruba porusza się w dół), to zwrot wektora \(\vec{c}\) obieramy w dół.

Regułę tę wytłumaczymy na poniższej animacji:

Animacja

Oznaczanie wektorów prostopadłych

Kartka papieru, ekran monitora są płaskie. Jak narysować wektor prostopadły do płaszczyzny, na którą patrzymy? Stosujemy następujące oznaczenia:

\(\odot\) — oznacza wektor prostopadły do płaszczyzny, na którą patrzysz, zwrócony do patrzącego,

\(\otimes\) — oznacza wektor prostopadły do płaszczyzny, na którą patrzysz, zwrócony za tę płaszczyznę.

Inne zagadnienia z tej lekcji

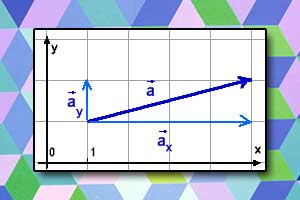Współrzędne wektora

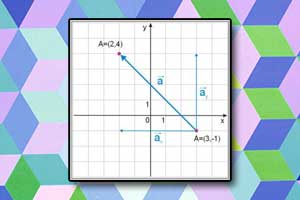Długość wektora

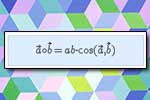Iloczyn skalarny

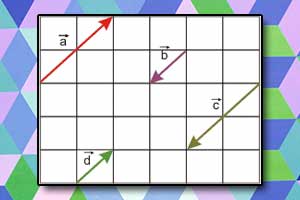Wektor

Mnożenie wektora przez liczbę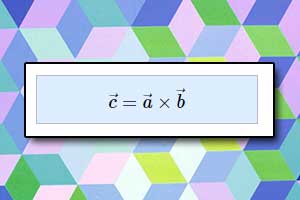

Iloczyn wektorowy

Pojęcie wektora

© medianauka.pl, 2017-02-11, A-3468
Data aktualizacji artykułu: 2023-07-15