Długość wektora

Jak obliczyć długość wektora? Podamy dwa wzory, w przypadku gdy dane są współrzędne tego wektora (składowe wektora), a także w przypadku gdy mamy dane współrzędne początku i końca wektora.

Długość wektora $\vec{a}$ (moduł wektora) będziemy oznaczać przez $|\vec{a}|$ lub a.

Aby obliczyć długość dowolnego wektora $\vec{a}$ będziemy korzystać ze wzoru:

$|\vec{a}|=\sqrt{a_x^2+a_y^2}$

gdzie a_x i a_y oznaczają miary składowych wektora $\vec{a}$ .

Zastosujmy powyższy wzór na długość wektora w zadaniu:

Przykład

Oto jak liczymy długość wektora $\vec{a}=[4,-3]$ :
$|\vec{a}|=\sqrt{4^2+(-3)^2}=\sqrt{16+9}=\sqrt{25}=5$

Gdy dane są jedynie współrzędne początku i końca wektora , to moduł wektora $\vec{AB}$ obliczymy ze wzoru:

$|\vec{AB}|=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$

Powyższy wzór wynika z własności współrzędnych wektora. Zauważ, że długość wektora obliczamy identycznie jak długość odcinka.

Przykład

Dany jest punkt A=(1,2) i B=(-2,3). Jaką długość ma wektor $\vec{AB}$ ?

Korzystamy z powyższego wzoru:

$|\vec{AB}|=\sqrt{(-2-1)^2+(3-2)^2}=\sqrt{3^2+1^2}=\sqrt{10}$

Zadania z rozwiązaniami

Zadania związane z tematem:
Długość wektora

Zadanie - długość wektora
Oblicz długość wektora:
$a) \ \vec{a}=[-3,4]\\ b) \ \vec{b}=5\vec{i}-2\vec{j}\\ c) \ \vec{c}=-\vec{j}\\ d)\ \vec{0}\\ e)\ \vec{AB}, \ A=(2,3), \ B=(-2,-3)$

Pokaż rozwiązanie zadania

Zadanie - długość wektora i równanie okręgu
Dany jest punkt A=(-1,1). Znaleźć punkt B jeżeli wiadomo, że $|\vec{AB}|=4$ .

Pokaż rozwiązanie zadania

Zadanie - długość wektora
Obliczyć długość wektora $\vec{a}=[1,1,1]$ .

Pokaż rozwiązanie zadania

Zadanie - mnożenie wektora przez skalar
Dany jest wektor $\vec{a}=[3,4]$ . Przez jaką liczbę należy go pomnożyć, aby jego długość była równa 1?

Pokaż rozwiązanie zadania

Inne zagadnienia z tej lekcji

Wektor
Co to jest wektor? Jakie ma własności?

Współrzędne wektora
Jak wyznaczamy Współrzędne wektora? Co to jest o wektor jednostkowy?

Suma wektorów
Poznasz metodę trójkąta, metodę graficzną dodawania wektorów, dodawanie i odejmowanie wektorów równoległych.

Odejmowanie wektorów
Opis odejmowania wektorów równoległych i nierównoległych.

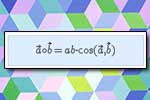Iloczyn skalarny
Co to jest iloczyn skalarny dwóch wektorów i jakie ma własności?

Mnożenie wektora przez liczbę
Definicja mnożenia wektora przez liczbę.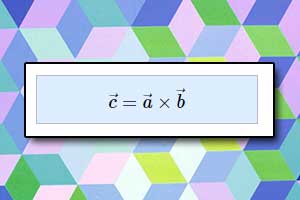

Iloczyn wektorowy
Iloczyn wektorowy - definicja i przykłady

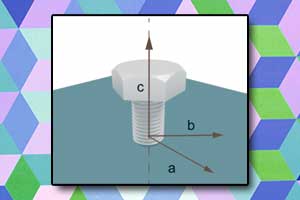Reguła śruby prawoskrętnej
Reguła śruby prawoskrętnej

Test wiedzy
Sprawdź swoje umiejętności z materiału zawartego w tej lekcji.