Iloczyn wektorowy
Co to jest iloczyn wektorowy? Na wstępie należy zaznaczyć, że nie jest to jedyny iloczyn dwóch wektorów. Iloczyn wektorowy daje w wyniku wektor, natomiast jest określone jeszcze tak zwany iloczyn skalarny, którego wynikiem jest liczba.
Definicja
Iloczyn wektorowy wektorów \(\vec{a}\) oraz \(\vec{b}\) nazywamy taki wektor \(\vec{c}\), że:
- jego kierunek jest prostopadły do płaszczyzny, na której leżą wektory \(\vec{a}\) i \(\vec{b}\),
- jego zwrot określa reguła śruby prawoskrętnej,
- jego długość jest równa \(a\cdot b\cdot \sin{\alpha}\), gdzie \(\alpha\) jest miarą kąta między tymi wektorami.
Iloczyn wektorowy oznaczamy następująco:
Iloczyn wektorowy — wzory
Podstawowy wzór przydatny w zadaniach z rachunku wektorowego jest następujący:
\(|\vec{a}\times \vec{b}|=|\vec{a}|\cdot |\vec{b}|\cdot \sin{\angle{(\vec{a},\vec{b})}}\)
Wzór ten pozwala wyznaczyć, jaką długość ma iloczyn wektorowy. Jest on równy iloczynowi długości dwóch wektorów i sinusowi kąta między nimi.
Zauważ, że w odróżnieniu od iloczynu skalarnego, wynikiem iloczynu wektorowego jest wektor, a nie skalar.
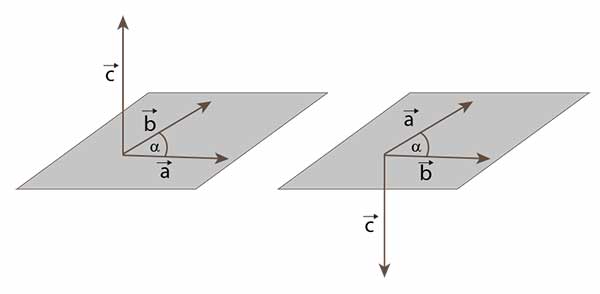
Własności iloczynu wektorowego
Uwaga! Iloczyn wektorowy nie jest przemienny.
Między współrzędnymi poszczególnych wektorów w iloczynie wektorowym zachodzą pewne zależności. Jeżeli \(\vec{c}=\vec{a}\times\vec{b}\), to:
\(\vec{a}=[a_x,a_y,a_z]\)
\(\vec{b}=[b_x,b_y,b_z]\)
\(\vec{c}=[c_x,c_y,c_z]\)
\(c_x=a_yb_z-a_zb_y\)
\(c_y=a_zb_x-a_xb_z\)
\(c_z=a_xb_y-a_yb_x\)
Prawo rozdzielności mnożenia wektorowego wektorów względem dodawania wektorów:
\(\vec{a}\times (\vec{b}+ \vec{c})=\vec{a}\times \vec{b}+\vec{a}\times \vec{c}\)
Prawo łączności mnożenia wektorowego wektorów przez skalar \(s\):
\(s(\vec{a}\times \vec{b})=(s\vec{a})\times \vec{b}\)
Oznaczanie wektorów prostopadłych
Jak narysować wektor prostopadły do płaszczyzny, na którą patrzymy? Stosuje się następujące oznaczenia:
\(\odot\) — oznacza wektor prostopadły do płaszczyzny, na którą patrzysz, zwrócony do patrzącego,
\(\otimes\) — oznacza wektor prostopadły do płaszczyzny, na którą patrzysz, zwrócony za tę płaszczyznę.
Pytania
Gdzie stosuje się iloczyn wektorowy?
Iloczyn wektorowy ma duże zastosowanie w fizyce — na przykład w ruchu obrotowym i w teorii pola elektromagnetycznego.
Powiązane materiały
© medianauka.pl, 2017-02-10, A-3467
Data aktualizacji artykułu: 2023-07-15

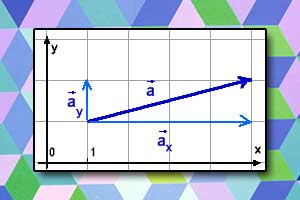 Współrzędne wektora
Współrzędne wektora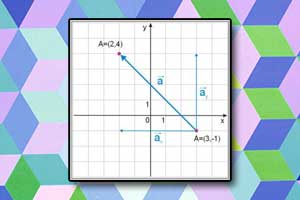 Długość wektora
Długość wektora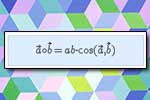 Iloczyn skalarny
Iloczyn skalarny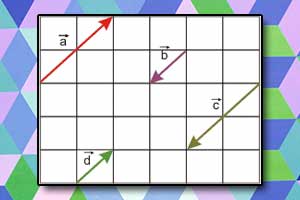 Wektor
Wektor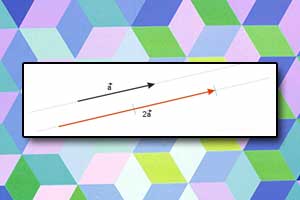 Mnożenie wektora przez liczbę
Mnożenie wektora przez liczbę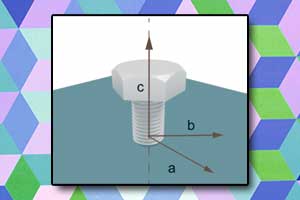 Reguła śruby prawoskrętnej
Reguła śruby prawoskrętnej Pojęcie wektora
Pojęcie wektora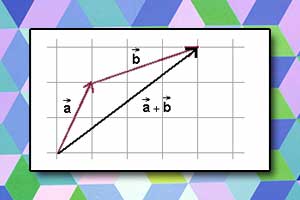 Suma wektorów
Suma wektorów Odejmowanie wektorów
Odejmowanie wektorów