Odejmowanie wektorów

Różnicę dwóch wektorów $\vec{a}$ i $\vec{b}$ możemy potraktować jako sumę wektora $\vec{a}$ oraz wektora przeciwnego do wektora $\vec{b}$ . Można to zapisać następująco:
$\vec{a}-\vec{b}=\vec{a}+(-\vec{b})$ . Możemy wówczas zastosować wcześniej poznane metody wyznaczania sumy wektorów.

Można też zastosować niżej opisaną metodę wyznaczania różnicy dwóch wektorów:

1) Za pomocą przesunięcia równoległego przesuwamy wektor $\vec{b}$ tak, aby początek wektora $\vec{b}$ znalazł się w początku wektora $\vec{a}$ .
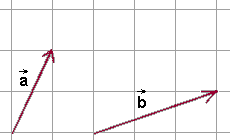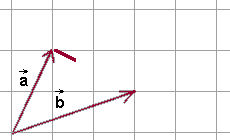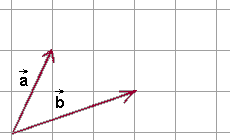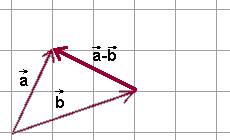
2) Różnicę wektorów $\vec{a}$ i $\vec{b}$ otrzymujemy łącząc końce obu wektorów $\vec{a}$ i $\vec{b}$ Zwrot wektora różnicy przyjmujemy do odjemnej.

Dokładnie taką samą zasadę stosujemy przy odejmowaniu wektorów równoległych. Ilustruje to poniższa animacja.

Przykład

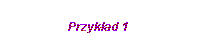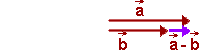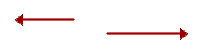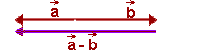
różnica wektorów równoległych - animacja

Różnica wektorów - wzór

Twierdzenie

Jeżeli $\vec{a}=[a_x,a_y],\ \vec{b}=[b_x,b_y], \ k\in R$ , to:

$\vec{a}-\vec{b}=[a_x-b_x,a_y-b_y]$

Przykład

Dane są wektory: $\vec{a}=[3,4], \ \vec{b}=[1,2]$ .

Obliczamy różnicę wektorów: $\vec{a}-\vec{b}=[3-1,4-2]=[2,2]$

Jeśli wektor jest wyrażony jako suma wersorów układu mnożonych przez odpowiednie współrzędne wektorów wówczas sumując je lub odejmując od siebie, sumujemy lub odejmujemy odpowiednie składowe wektorów, grupując je.

Zadania z rozwiązaniami

Zadania związane z tematem:
Odejmowanie wektorów

Zadanie - odejmowanie wektorów
Znaleźć graficznie różnicę wektorów $\vec{a}=[2,-3], \ \vec{b}=[-2,-3]$

Pokaż rozwiązanie zadania

Zadanie - różnica wektorów
Dane są wektory $\vec{a}, \ \vec{b}$ pokazane na poniższym rysunku. Znaleźć graficznie wektor $\vec{c}$ taki, że $\vec{b}-\vec{c}=\vec{a}$
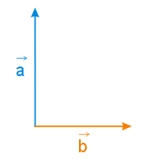
Wektory

Pokaż rozwiązanie zadania

Zadanie - odejmowanie wektorów
Dany jest trapez równoramienny ABCD. Znaleźć graficznie wektory:
$\vec{a}=\vec{AB}-\vec{BC}, \ \vec{b}=\vec{AB}-\vec{CD}, \ \vec{c}=\vec{BC}-\vec{AD}$

Pokaż rozwiązanie zadania

Zadanie - odejmowanie wektorów
Dany jest prostokąt ABCD. Znaleźć graficznie wektor $\vec{AB}-\vec{AD}-\vec{CA}-\vec{DC}$

Pokaż rozwiązanie zadania

Zadanie - działania na współrzędnych wektora
Dany jest wektor $\vec{a}=[2,4]$ .Jakie współrzędne ma wektor $\vec{b}$ , jeżeli wiadomo, że $\vec{a}-\vec{b}=[7,7]$ ?

Pokaż rozwiązanie zadania

Zadanie - działania na wektorach równoległych
Dany jest prostokąt ABCD. Znaleźć graficznie wektory
$\vec{AB}+\vec{DC}, \ \vec{BC}+\vec{DA},\ \vec{DA}-\vec{BC}, \ \vec{CD}-\vec{BA}$

Pokaż rozwiązanie zadania

Inne zagadnienia z tej lekcji

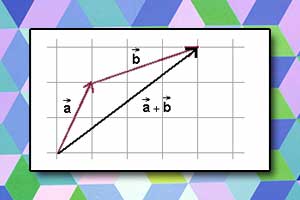Suma wektorów
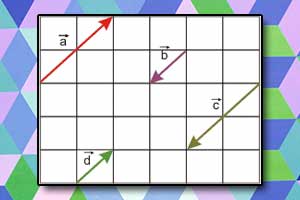Poznasz metodę trójkąta, metodę graficzną dodawania wektorów, dodawanie i odejmowanie wektorów równoległych.

Wektor
Co to jest wektor? Jakie ma własności?

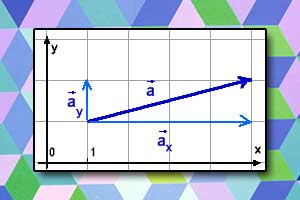Współrzędne wektora
Jak wyznaczamy Współrzędne wektora? Co to jest o wektor jednostkowy?

Długość wektora
Jak obliczyć długość dowolnego wektora?

Suma wektorów
Poznasz metodę trójkąta, metodę graficzną dodawania wektorów, dodawanie i odejmowanie wektorów równoległych.

Iloczyn skalarny
Co to jest iloczyn skalarny dwóch wektorów i jakie ma własności?

Mnożenie wektora przez liczbę
Definicja mnożenia wektora przez liczbę.

Iloczyn wektorowy
Iloczyn wektorowy - definicja i przykłady

Reguła śruby prawoskrętnej
Reguła śruby prawoskrętnej

Test wiedzy