Zadanie - działania na współrzędnych wektora
Treść zadania:
Dany jest wektor \(\vec{a}=[2,4]\). Jakie współrzędne ma wektor \(\vec{b}\), jeżeli wiadomo, że \(\vec{a}-\vec{b}=[7,7]\)?
Rozwiązanie zadania
Jeżeli \(\vec{a}=[a_x,a_y],\ \vec{b}=[b_x,b_y], \ k\in R\), to:
\(\vec{a}+\vec{b}=[a_x+b_x,a_y+b_y]\)\(\vec{a}-\vec{b}=[a_x-b_x,a_y-b_y]\)
\(k\vec{a}=[ka_x,ka_y]\)
Niech \(\vec{b}=[x,y]\). Mamy więc:
\(\vec{a}-\vec{b}=[2,4]-[x,y]=[2-x,4-y]\)
Wiemy, że różnica obu wektorów ma współrzędne \([7,7],\) więc:
\([2-x,4-y]=[7,7]\)
\(2-x=7\)
\(-x=7-2/\cdot (-1)\)
\(x=-5\)
\(4-y=7\)
\(-y=7-4/\cdot (-1)\)
\(y=-3\)
\(\vec{b}=[-5,-3]\)
Odpowiedź
\(\vec{b}=[-5,-3]\)© medianauka.pl, 2011-03-11, ZAD-1211


Zadania podobne
Zadanie nr 1.
Znaleźć graficznie różnicę wektorów \(\vec{a}=[2,-3], \vec{b}=[-2,-3]\),
Zadanie nr 2.
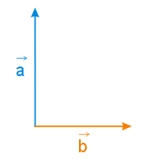
Dane są wektory \(\vec{a}, \vec{b}\), pokazane na poniższym rysunku. Znaleźć graficznie wektor \(\vec{c}\) taki, że \(\vec{b}-\vec{c}=\vec{a}\).
Zadanie nr 3.
Dany jest trapez równoramienny \(ABCD\). Znaleźć graficznie wektory:
\(\vec{a}=\vec{AB}-\vec{BC}, \vec{b}=\vec{AB}-\vec{CD}, \vec{c}=\vec{BC}-\vec{AD}\)
Zadanie nr 4.
Dany jest prostokąt \(ABCD\). Znaleźć graficznie wektor \(\vec{AB}-\vec{AD}-\vec{CA}-\vec{DC}\).
Zadanie nr 5.
Dany jest prostokąt \(ABCD\). Znaleźć graficznie wektory \(\vec{AB}+\vec{DC}, \vec{BC}+\vec{DA}, \vec{DA}-\vec{BC}, \vec{CD}-\vec{BA}\).

