Logo Media Nauka

Facebook

Dodawanie wektorów

Wektory podlegają podobnym działaniom jak skalary, jednak zasady dodawania i odejmowania wektorów zasadniczo różnią się od sposobu dodawania i odejmowania liczb.

Warto poznać różne metody działań na wektorach, zarówno graficzne jak i algebraiczne. Zostaną one opisane w kolejnych częściach lekcji.

Poznasz więc metodę trójkąta, metodę graficzną dodawania wektorów, dodawanie i odejmowanie wektorów równoległych. W niniejszej lekcji zostały również omówione działania na współrzędnych wektorów.

Suma wektorów metodą trójkąta

Jest to geometryczna metoda dodawania wektorów.

suma wektorów, dodawanie wektorów - metoda trójkąta - animacja
  1. Za pomocą przesunięcia równoległego przesuwamy wektor\vec{b} tak, aby początek wektora \vec{b} znalazł się w końcu wektora \vec{a}.
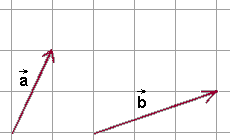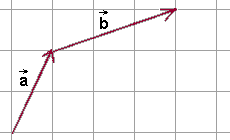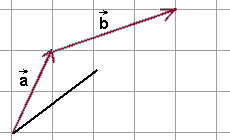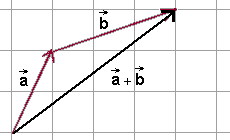
  2. Sumę wektorów \vec{a} i \vec{b} otrzymujemy łącząc początek wektora \vec{a} z końcem wektora \vec{b}

Dodawanie wektorów metodą równoległoboku

Jest to również geometryczna metoda dodawania wektorów.

metoda równoległoboku - animacja
  1. Za pomocą przesunięcia równoległego przesuwamy wektor \vec{b} tak, aby początek wektora \vec{b} znalazł się w początku wektora \vec{a}.
  2. Budujemy równoległobok oparty o wektory \vec{a} i \vec{b}.
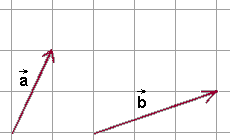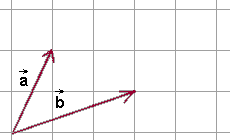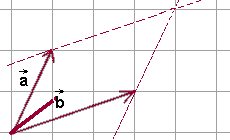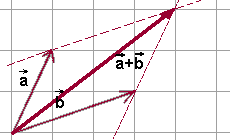
  3. Sumę wektorów \vec{a} i \vec{b} otrzymujemy łącząc początek wektorów \vec{a} i \vec{b} naprzeciwległym wierzchołkiem równoległoboku.

Suma wielu wektorów - metoda graficzna

suma wielu wektorów - animacja 1) Za pomocą przesunięcia równoległego przesuwamy wektory tak, aby początek kolejnego wektora znajdował się w końcu poprzedniego wektora. Tworzymy w ten sposób "łańcuch" wektorów.
2) Sumę wektorów otrzymujemy łącząc początek pierwszego wektora z końcem ostatniego.

Dodawanie wektorów równoległych

Teoria Wektory równoległe najłatwiej dodawać stosując metodę trójkąta, czyli do końca jednego wektora przesuwamy początek drugiego. Sumę wektorów otrzymujemy łącząc początek pierwszego z końcem drugiego wektora. Oto dwa przykłady:

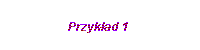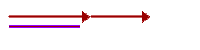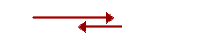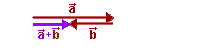
suma wektorów równoległych - animacja

Dodawanie wektorów - wzór

Jeżeli mamy dane współrzędne wektorów, to prawdziwe jest twierdzenie:

Twierdzenie Twierdzenie

Jeżeli \vec{a}=[a_x,a_y],\ \vec{b}=[b_x,b_y], \ k\in R, to:

\vec{a}+\vec{b}=[a_x+b_x,a_y+b_y]

Przykład Przykład

Dane są wektory:\vec{a}=[3,4], \ \vec{b}=[1,2].

Obliczamy sumę wektorów: \vec{a}+\vec{b}=[3+1,4+2]=[4,6]

Teoria Jeśli wektor jest wyrażony jako suma wersorów układu mnożonych przez odpowiednie współrzędne wektorów wówczas sumując je lub odejmując od siebie, sumujemy lub odejmujemy odpowiednie składowe wektorów, grupując je.

Przykład Przykład

Dane są wektory:
\vec{a}=5\vec{i}-2\vec{j}\\ \vec{b}=-2\vec{i}+2\vec{j}
Znaleźć sumę tych wektorów.

Wykonujemy więc dodawanie wektorów:

\vec{a}+\vec{b}=5\vec{i}-2\vec{j}+(-2\vec{i}+2\vec{j})=5\vec{i}-2\vec{i}-2\vec{j}+2\vec{j}=\\ =(5-2)\vec{i}+(-2+2)\vec{j}=3\vec{i}+0\cdot \vec{j}=3\vec{i}



© medianauka.pl, 2008-04-25, ART-26


Zadania z rozwiązaniami

spis treści
Zadania związane z tematem:
Suma wektorów

zadanie-ikonka Zadanie - Dodawanie wektorów metodą trójkata
Dany jest prostokąt ABCD. Zaznacz na rysunku wektory
\vec{a}=\vec{AB}+\vec{BC},\ \vec{b}=\vec{AD}+\vec{BA},\\ \vec{c}=\vec{DC}+\vec{AB},\ \vec{d}=\vec{AB}+\vec{CB}

Pokaż rozwiązanie zadania

zadanie-ikonka Zadanie - Dodawanie wektorów
Dany jest trapez równoramienny ABCD. Zaznacz na rysunku wektory
\vec{a}=\vec{AB}+\vec{BC},\ \vec{b}=\vec{AB}+\vec{BC}+\vec{CD},\\ \vec{c}=\vec{AB}+\vec{BC}+\vec{CD}+\vec{DA},\ \vec{d}=\vec{AB}+\vec{BC}+\vec{DC}

Pokaż rozwiązanie zadania

zadanie-ikonka Zadanie - dodawanie wektorów metodą trójkąta
Dane są wektory \vec{a}, \ \vec{b} pokazane na poniższym rysunku. Znaleźć graficznie wektor \vec{c}, jeżeli wiadomo, że \vec{a}+\vec{c}=\vec{b}
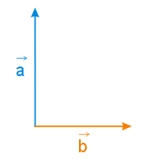
Wektory

Pokaż rozwiązanie zadania

zadanie-ikonka Zadanie - dodawanie wektorów
Znaleźć graficznie sumę wektorów \vec{a}=[-2,3], \ \vec{b}=[2,1],
a) metodą trójkąta
b) metodą równoległoboku.

Pokaż rozwiązanie zadania

zadanie-ikonka Zadanie - działania na wektorach
Dane są wektory \vec{a}=[-2,3], \ \vec{b}=[3,-3], \vec{c}=[2,4]. Znaleźć:
\vec{a}+\vec{b},\ -\vec{a}+\vec{c},\ \vec{a}+\vec{b}+\vec{c},\ \vec{b}-\vec{a},\ \vec{c}-\vec{a}+\vec{b},\ 5\vec{a}-3\vec{b}

Pokaż rozwiązanie zadania

zadanie-ikonka Zadanie - działania na współrzędnych wektorów
Dane są wektory \vec{a}=-5\vec{i}+6\vec{j}, \ \vec{b}=3\vec{i}-4\vec{j}, \ \vec{c}=\vec{i}-4\vec{j}.
Oblicz \vec{a}+\vec{b}, \ \vec{c}+\vec{b},\ \vec{a}+\vec{b}-\vec{c}

Pokaż rozwiązanie zadania

zadanie-ikonka Zadanie - dodawanie wektorów metodą równoległoboku
Dany jest trapez równoramienny ABCD. Znaleźć graficznie metodą równoległoboku wektor \vec{AD}+\vec{BC} (sumę wektorów wyznaczonych przez ramiona trapezu).

Pokaż rozwiązanie zadania

zadanie-ikonka Zadanie - dodawanie wektorów metodą równoległoboku
Dany jest trójkąt prostokątny ABC. Znaleźć graficznie metodą równoległoboku wektor:
a) \vec{AB}+\vec{BC}+\vec{AC}
b) \vec{CA}+\vec{BC}

Pokaż rozwiązanie zadania

zadanie-ikonka Zadanie - działania na wektorach równoległych
Dany jest prostokąt ABCD. Znaleźć graficznie wektory
\vec{AB}+\vec{DC}, \ \vec{BC}+\vec{DA},\ \vec{DA}-\vec{BC}, \ \vec{CD}-\vec{BA}

Pokaż rozwiązanie zadania



Inne zagadnienia z tej lekcji

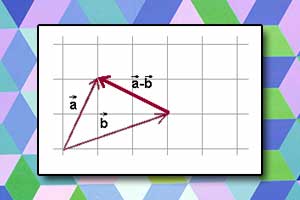Odejmowanie wektorówOdejmowanie wektorów
Opis odejmowania wektorów równoległych i nierównoległych.
WektorWektor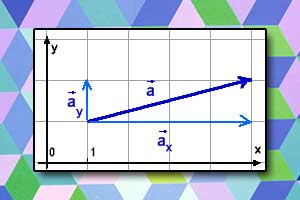
Co to jest wektor? Jakie ma własności?
Współrzędne wektoraWspółrzędne wektora
Jak wyznaczamy Współrzędne wektora? Co to jest o wektor jednostkowy?
Długość wektoraDługość wektora
Jak obliczyć długość dowolnego wektora?
Odejmowanie wektorówOdejmowanie wektorów
Opis odejmowania wektorów równoległych i nierównoległych.
Iloczyn skalarnyIloczyn skalarny
Co to jest iloczyn skalarny dwóch wektorów i jakie ma własności?
Mnożenie wektora przez liczbęMnożenie wektora przez liczbę
Definicja mnożenia wektora przez liczbę.
Iloczyn wektorowyIloczyn wektorowy
Iloczyn wektorowy - definicja i przykłady
Reguła śruby prawoskrętnejReguła śruby prawoskrętnej
Reguła śruby prawoskrętnej
TestTest wiedzy
Sprawdź swoje umiejętności z materiału zawartego w tej lekcji.

Jak mrówki nawigują i co mają z tym wspólnego wektory?

Jak mrówki nawigują i co mają z tym wspólnego wektory?

Istnieje pewien rodzaj mrówek, który posługuje się specyficznym sposobem orientowania się w przestrzeni. Czy ma to coś wspólnego z wektorami? Otóż okazuje się, że tak!








Polecamy w naszym sklepie

Kolorowe skarpetki 3D
cyferki - gra - trefl
Algebra
Kolorowe skarpetki - czarno-białe grochy
laboratorium w szufladzie Matematyka
Niektóre treści nie są dostosowane do Twojego profilu. Jeżeli jesteś pełnoletni możesz wyrazić zgodę na przetwarzanie swoich danych osobowych. W ten sposób będziesz miał także wpływ na rozwój naszego serwisu.
© ® Media Nauka 2008-2021 r.