Współrzędne wektora
Współrzędne wektora
Współrzędne wektora to miary wektorów składowych.
Wersor
To wektor jednostkowy, wektor o długości jednostkowej, którego zwrot jest zgodny ze zwrotem prostej, na której leży.Zaczniemy od wyjaśnienia, co to jest wektor jednostkowy (wersor).
Wektor jednostkowy — wersor
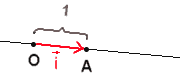
Dana jest prosta, na której zaznaczono dwa punkty: \(O\) i \(A\). Zwrot prostej jest od \(O\) do \(A\). Jeżeli przyjmiemy, że odcinek \(OA\) jest jednostką długości (\(OA=1\)), to wektor \(\vec{OA}\) nazywać będziemy wersorem (wektorem jednostkowym).
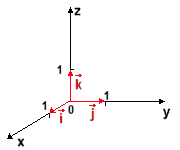
Wersory układu kartezjańskiego zwykło się oznaczać przez \(\vec{i},\ \vec{j},\ \vec{k}\).
Miara wektora
Miarą wektora \(\vec{a}\) na osi \(OX\) nazywać będziemy liczbę \(a_x\) równą długości tego wektora wziętej ze znakiem „plus”, jeżeli zwrot wektora jest zgodny ze zwrotem osi \(OX\), natomiast ze znakiem „minus”, jeżeli zwrot wektora jest przeciwny do zwrotu osi \(OX\).
Przykład
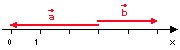
W zilustrowanym powyżej przykładzie miarą wektora \(\vec{a}\) jest liczba \(-3\), natomiast miarą wektora \(\vec{b}\) jest liczba \(2\).
Współrzędne wektora
Współrzędne wektora zdefiniujemy jako miary wszystkich wektorów składowych.
Współrzędne wektora zapisujemy w nawiasach kwadratowych.
Przykład 1
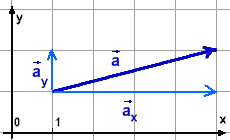
W powyższym przykładzie \(\vec{a}=[4,1]\), gdyż miarą składowej \(\vec{a_x}\) jest liczba \(4\), natomiast miarą składowej \(\vec{a_y}\) jest liczba \(1\).
Przykład 2
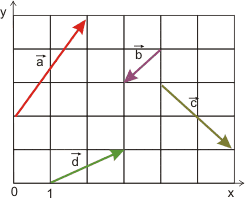
Wektory zilustrowane na powyższym rysunku mają następujące współrzędne:
\(\vec{a}=[2,3]\)
\(\vec{b}=[-1,-1]\)
\(\vec{c}=[2,-2]\)
\(\vec{d}=[2,1]\)
Własności współrzędnych wektorów
Twierdzenie 1
Jeśli wektor \(\vec{a}=\vec{AB}\) leży na osi \(OX\), to zachodzi równość: \(a_x=x_B-x_A\).
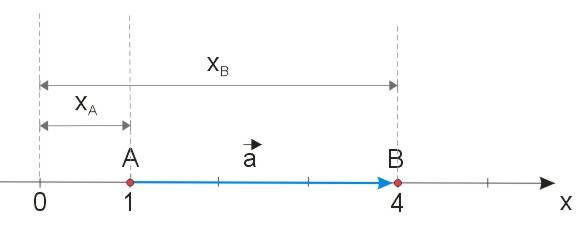
Przykład
Punkt \(A\) ma współrzędną równą \(-2\) na osi \(OX\), punkt \(B\) ma współrzędną \(2\). Jaka jest współrzędna wektora \(\vec{a}=\vec{AB}\)?
Korzystamy z powyższego twierdzenia i mamy: \(a_x=x_B-x_A=2-(-2)=4\)
Twierdzenie 2
Dowolny wektor na płaszczyźnie można przedstawić jako sumę wersorów układu pomnożonych przez odpowiednie współrzędne wektora: \(\vec{v}=v_x\vec{i}+v_y\vec{j}\)
Twierdzenie 3
Dowolny wektor w przestrzeni można przedstawić jako sumę wersorów układu pomnożonych przez odpowiednie współrzędne wektora: \(vec{v}=v_x\vec{i}+v_y\vec{j}+v_z\vec{k}\)
Przykład
Wektor \(\vec{a}=[-2,1,8]\) można przedstawić jako \(\vec{a}=-2\vec{i}+\vec{j}+8\vec{k}\).
Twierdzenie 4
Jeżeli wektor \(\vec{a}=\vec{AB}\) leży na płaszczyźnie \(OXY\), to zachodzą równości:
\(a_x=x_B-x_A\)
\(a_y=y_B-y_A\)
Powyższe twierdzenie pozwala nam wyznaczyć w prosty sposób współrzędne wektora, gdy dane są współrzędne jego początku i końca.
Przykład
Dane są punkty \(A=(3,-1)\) oraz \(B=(-2,4)\). Wyznaczyć współrzędne wektora \(\vec{a}=\vec{AB}\).
Korzystamy z powyższego twierdzenia i mamy:
\(a_x=x_B-x_A=-2-3=-5\)
\(a_y=y_B-y_A=4-(-1)=5\)
Mamy więc: \(\vec{a}=[-5,5]\)
Zilustrujemy to jeszcze rysunkiem.

Działania na współrzędnych wektorów
Jeżeli \(\vec{a}=[a_x,a_y],\ \vec{b}=[b_x,b_y], \ k\in \mathbb{R}\), to:
\(\vec{a}+\vec{b}=[a_x+b_x,a_y+b_y]\)
\(\vec{a}-\vec{b}=[a_x-b_x,a_y-b_y]\)
\(k\vec{a}=[ka_x,ka_y]\)
Przykłady
Dane są wektory: \(\vec{a}=[3,4], \ \vec{b}=[1,2]\).
- Obliczamy sumę wektorów: \(\vec{a}+\vec{b}=[3+1,4+2]=[4,6]\)
- Obliczamy różnicę wektorów: \(\vec{a}-\vec{b}=[3-1,4-2]=[2,2]\)
- Obliczamy różnicę wektorów: \(\vec{b}-\vec{a}=[1-3,2-4]=[-2,-2]\)
- Obliczamy iloczyn wektora przez liczbę \(k=2\): \(2\vec{a}=2\cdot [3,4]=[2\cdot 3,2\cdot 4]=[6,8]\)
Jeśli wektor jest wyrażony jako suma wersorów układu mnożonych przez odpowiednie współrzędne wektorów, wówczas sumując je lub odejmując od siebie, sumujemy lub odejmujemy odpowiednie składowe wektorów, grupując je.
Przykład
Dane są wektory:
\(\vec{a}=5\vec{i}-2\vec{j}, \vec{b}=-2\vec{i}+2\vec{j}\)
Znaleźć sumę tych wektorów.
Wykonujemy więc dodawanie:
\(\vec{a}+\vec{b}=5\vec{i}-2\vec{j}+(-2\vec{i}+2\vec{j})=5\vec{i}-2\vec{i}-2\vec{j}+2\vec{j}=\)
\( =(5-2)\vec{i}+(-2+2)\vec{j}=3\vec{i}+0\cdot \vec{j}=3\vec{i}\)
Pytania
Jak obliczyć współrzędne wektora?
Wyżej opisujemy analityczny sposób określania współrzędnych wektora. Tu pozwolimy sobie na bardziej swobodny opis. Spójrzmy na rysunek.

Aby obliczyć współrzędne naszego wektora \(\vec{a}=\vec{AB}\) wystarczy naszkicować sobie jego składowe i określić ich długość, a znak przyjąć zgodny ze zwrotem osi. Tu składowa \(x\) ma \(5\) jednostek, jest zwrócona przeciwnie do osi \(OX\), a składowa \(y\) ma również \(5\) jednostek, a jej zwrot jest zgodny z osią \(OY\). Stąd nasz wektor ma współrzędne \([-5,5]\).
Jaki jest wzór na długość wektora?
Długość wektora omawiamy w kolejnym artykule, tu jednak podamy odpowiednie wzory:
\(|\vec{a}|=\sqrt{a_x^2+a_y^2}\)
\(|\vec{AB}|=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\)
Zadania z rozwiązaniami

Zadanie nr 1.
Dane są punkty \(A=(3,-5), B=(1,5), C=(-3,2)\). Znaleźć współrzędne wektorów \(\vec{AB}, \ \vec{BA},\ \vec{AC},\ \vec{CB}\).

Zadanie nr 2.
Zaznaczyć w układzie współrzędnych wektory zaczepione w punkcie \(A=(1,1)\), określone następująco:
\(\vec{a}=[1,3]\)
\(\vec{b}=[-1,2]\)
\(\vec{c}=2\vec{i}-3\vec{j}\)
\(\vec{d}=\vec{i}-\vec{j}\)
\(\vec{e}=5\vec{i}\)
\(\vec{f}=-\vec{j}\)

Zadanie nr 3.
Znaleźć współrzędne punktu \(B\), jeżeli wiadomo, że \(A=(2,2)\) i
a) \(\vec{AB}=[-2,-3]\)
b) \(\vec{AB}=2\vec{i}+4\vec{j}\)

Zadanie nr 4.
Dany jest prostokąt \(ABCD\), gdzie \(A=(1,1), B=(5,1), C=(5,3), D=(1,3)\). Znaleźć współrzędne wektorów \(\vec{AD}, \vec{CA}, \vec{BD}, \vec{CD}\).
Powiązane materiały
 Współrzędne wektorów
Współrzędne wektorów© medianauka.pl, 2008-04-23, A-22
Data aktualizacji artykułu: 2023-07-09

 Wektor
Wektor Długość wektora
Długość wektora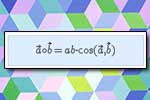 Iloczyn skalarny
Iloczyn skalarny Mnożenie wektora przez liczbę
Mnożenie wektora przez liczbę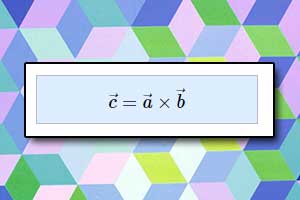 Iloczyn wektorowy
Iloczyn wektorowy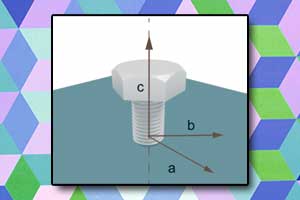 Reguła śruby prawoskrętnej
Reguła śruby prawoskrętnej Pojęcie wektora
Pojęcie wektora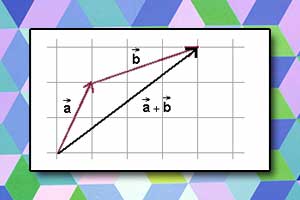 Suma wektorów
Suma wektorów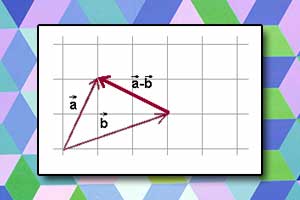 Odejmowanie wektorów
Odejmowanie wektorów