Całka nieoznaczona
Całka to pojęcie ogólne, które w analizie matematycznej oznacza całkę oznaczoną, nieoznaczoną lub inny rodzaj całki. Całki można sobie wyobrazić jako operacje sumowania nieskończenie wielu bardzo małych wartości. To podejście poglądowe, jednak istotna jest ścisła definicja poszczególnych całek.
Funkcja pierwotna
Jeżeli pewna funkcja \(f(x)\) jest określona w przedziale \((a;b)\), to:
Definicja
Funkcja \(F(x)\) jest funkcją pierwotną funkcji \(f(x)\) w przedziale \((a;b)\), jeżeli \(F'(x)=f(x)\) dla każdego \(x\) z tego przedziału.
Przykład
Funkcja \(f(x)=x^3\) to funkcja pierwotna w stosunku do funkcji \(3x^2\) w zbiorze liczb rzeczywistych, ponieważ \((x^3)'=3x^2\).
Zauważmy jednak, że funkcje \(x^3+3\), \(x^3-100\), ogólnie \(x^3+C\), gdzie \(C\) jest liczbą stałą, również są funkcjami pierwotnymi funkcji \(f(x)=3x^2\) w zbiorze liczb rzeczywistych.
Całka nieoznaczona — definicja
Całką nieoznaczoną (nieokreśloną) funkcji \(f(x)\) nazywamy wyrażenie \(F(x)+C\). Całkę funkcji \(f(x)\) oznaczamy następująco:
Wielkość \(C\) jest dowolną liczbą, \(F(x)\) — funkcją pierwotną funkcji \(f(x)\), którą nazywamy funkcją podcałkową, \(x\) nazywamy zmienną całkowania. Znak \(dx\) jest częścią symbolu całkowania i wskazuje na to, po jakiej zmiennej należy całkować funkcję podcałkową.
Przykłady całek
- \(\int xdx=\frac{1}{2}x^2+C\), bo \((\frac{1}{2}x^2+C)'=\frac{1}{2}\cdot 2x+0=x\)
- \(\int \sin{2x}dx=\sin^2{x}+C\), bo \((\sin^2{x}+C)' =2\sin{x}\cdot{}\cos{x}+0=\sin{2x}\)
W kolejnych artykułach poznamy podstawowe wzory całkowania, które ułatwią rachunek całkowy.
Całkowanie, podobnie jak obliczanie pochodnej, ma ogromne zastosowanie w fizyce, chemii, matematyce i innych naukach.
Całka nieoznaczona — wzory
W niniejszym artykule zostaną przedstawione podstawowe wzory rachunku całkowego wraz z przykładami ich stosowania:
- \(\int{dx}=x+C\)
- \(\int{kdx}=kx+C\)
- \(\int{x^ndx}=\frac{x^{n+1}}{n+1}+C, a\neq-1, x>0\)
- \(\int{\frac{1}{x}dx}=\ln{|x|}+C, x\neq{0}\)
- \(\int{e^xdx}=e^x+C\)
- \(\int{a^xdx}=\frac{a^x}{\ln{a}}+C, a>0, a\neq{1}\)
- \(\int{\sin{x}dx}=-\cos{x}+C\)
- \(\int{\cos{x}dx}=\sin{x}+C\)
- \(\int{\frac{1}{\cos^{2}{x}}dx}=tgx+C, \cos{x}\neq{0}\)
- \(\int{\frac{1}{\sin^{2}{x}}dx}=-ctgx+C, \sin{x}\neq{0}\)
- \(\int{\frac{1}{\sqrt{1-x^2}}dx}=arcsinx+C,\quad{}-1<x<1\)
- \(\int{\frac{1}{x^2+1}dx}=arctg+C\)
Przykłady
\(\int{5dx}=5x+C\)
\(\int{-2dx}=-2x+C\)
\(\int{xdx}=\int{x^1dx}=\frac{x^{1+1}}{1+1}+C=\frac{1}{2}x^2+C\)
\(\int{x^2dx}=\frac{x^{2+1}}{2+1}+C=\frac{1}{3}x^3+C\)
\({\int{\frac{1}{x^2}dx}=\int{x^{-2}dx}=\frac{x^{-2+1}}{-2+1}+C=-x^{-1}+C=-\frac{1}{x}+C}\)
\(\int{5^xdx}=\frac{5^x}{\ln{5}}+C\)
Własności całek nieoznaczonych
Obliczanie całek nieoznaczonych nie jest łatwą czynnością. Przydatne przy tym będą poniższe wzory:
Całka sumy jest równa sumie całek.
Przykłady
Obliczymy całkę na podstawie powyższej własności:
\(\int{(4x+1)}dx =\int{4xdx}+\int{1dx} = 4\cdot{\frac{1}{2}x^2}+1\cdot{x}+C =2x^2+x+C\)
Dla \(k\) różnego od zera, czynnik stały można wyłączyć przed znak całki.
Przykład
Obliczymy całkę, korzystając z powyższej własności:
\(\int{3\sqrt{x}}dx= 3\int{\sqrt{x}dx}=3\int{x^{ \frac{1}{2}}dx}= 3\cdot {\frac{x^{\frac{1}{2}+1}}{ \frac{1}{2}+1}}+C=\)
\(=3\cdot\frac{x^{\frac{3}{2}}}{ \frac{3}{2}}+C= 3\cdot \frac{2}{3}\sqrt{x^3}+C=2\sqrt{x^3}+C\)
Dzięki powyższym własnościom możemy całkę „rozbijać” na kilka całek, kiedy mamy do czynienia z całką różnicy funkcji. Pamiętać należy, że nie możemy tego robić w przypadku, kiedy mamy do czynienia z całką iloczynu oraz całką ilorazu funkcji. W takim przypadku stosuje się inne metody rachunku całkowego, między innymi całkowanie przez części oraz metodę podstawienia, które zostaną omówione w kolejnych artykułach.
Pytania
Jakie jest zastosowanie całek w praktyce?
Jak wynika z podejścia poglądowego do zrozumienia całki, o którym piszemy na wstępie, całki można wykorzystać do obliczania pól powierzchni pod krzywą. Rachunek całkowy jest też szeroko wykorzystywany w fizyce, technice, naukach przyrodniczych i ekonomicznych.
Czy wszystkie funkcje można całkować?
Nie. Funkcja z całą pewnością jednak jest całkowalna w danym przedziale, jeżeli:
- jest w tym przedziale ciągła,
- jest w tym przedziale monotoniczna,
- jeżeli dana funkcja jest ograniczona w tym przedziale i ma w tym przedziale skończoną liczbę nieciągłości.
Wszystkie funkcje wymierne i trygonometryczne są całkowalne.
Przykładem funkcji, która nie jest całkowalna w przedziale \(\langle0;1\rangle\) jest funkcja Dirichleta (określona w taki sposób, że przejmuje wartość 1 dla liczb wymiernych i 0 dla pozostałych liczb).
Zadania z rozwiązaniami

Zadanie nr 1.
Oblicz:
a) \(\int \frac{dx}{\sqrt{x}}\)
b) \(\int \sqrt{x}dx\)
Powiązane materiały
© medianauka.pl, 2010-10-09, A-952
Data aktualizacji artykułu: 2023-05-19

 Całkowanie przez podstawienie
Całkowanie przez podstawienie Całkowanie przez części
Całkowanie przez części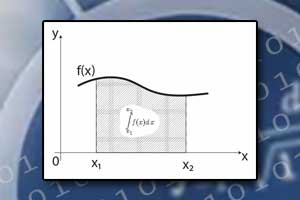 Całka oznaczona
Całka oznaczona Całka nieoznaczona
Całka nieoznaczona