Całka oznaczona

Definicja

Jeżeli \(F(x)\) jest funkcją pierwotną funkcji \(f(x)\) ciągłej w danym przedziale \(\langle x_1;x_2\rangle\), to różnicę funkcji pierwotnych \(F(x_2)\) i \(F(x_1)\) nazywamy całką oznaczoną dla funkcji \(f\) od \(x_1\) do \(x_2\).

Wzór

Stosujemy następujące zapisy i oznaczenia dla całek oznaczonych:

\(\displaystyle\int_{x_1}^{x_2}f(x)dx=F(x_2)-F(x_1)\)

lub

\(\displaystyle\int_{x_1}^{x_2}f(x)dx=[F(x)]^{x_2}_{x_1}\)

Powyższe zapisy możemy przeczytać następująco:

Całka oznaczona funkcji \(f(x)\) po \(dx\) w granicach \(x_1\) do \(x_2\) jest równa \(F(x)\) z podstawieniem \(x_2\) od góry (górnym) i \(x_1\) od dołu (dolnym).

Obliczanie całek oznaczonych warto prześledzić na przykładach.

Przykłady

Jeżeli potrafimy wyznaczać całki nieoznaczone, to obliczenie całki oznaczonej polega na obliczeniu różnicy wartości znalezionych funkcji pierwotnych dla wskazanych punktów przedziału. Zauważmy, że ponieważ obliczamy różnicę tych samych funkcji pierwotnych, ale w różnych punktach, stała \(C\) z funkcji pierwotnej redukuje się.

Obliczmy przykładowe całki oznaczone:

\(\displaystyle\int_{0}^{1}2xdx = [x^2]^{1}_{0}=1^2-0^2=1\)

\(\displaystyle\int_{1}^{3}x^2dx = [\frac{x^3}{3}]^{3}_{1}=9-\frac{1}{3}=\frac{26}{3}\)

Własności całek oznaczonych

Wprost z definicji zachodzą następujące własności:

\(\displaystyle\int_{x_1}^{x_1}f(x)dx=0\)

oraz

\(\displaystyle\int_{x_1}^{x_2}f(x)dx=- \int_{x_2}^{x_1}f(x)dx\)

Interpretacja geometryczna całki oznaczonej

Całka oznaczona jest równa polu powierzchni pod krzywą opisanej funkcją \(f(x)\) w granicach ograniczonej przedziałem \(\langle x_1;x_2\rangle\) zgodnie z rysunkiem.

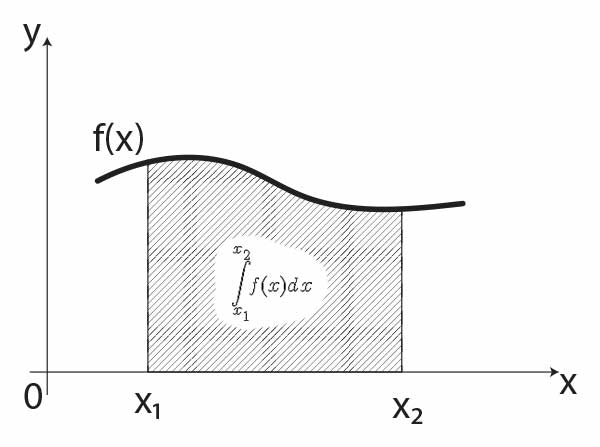
całka oznaczona

Z tego chociażby powodu całki oznaczone znajdują zastosowanie w geometrii. Można nie tylko wyznaczyć wartość pola powierzchni, ale nawet wzór na pole powierzchni wybranej figury geometrycznej. Rachunek całkowy jest wykorzystywany także często w fizyce.